CF1899F Alex's whims
· One min read



解题思路
如图,用 个节点构造一条链,根节点为 ,叶节点为 。(图中 )
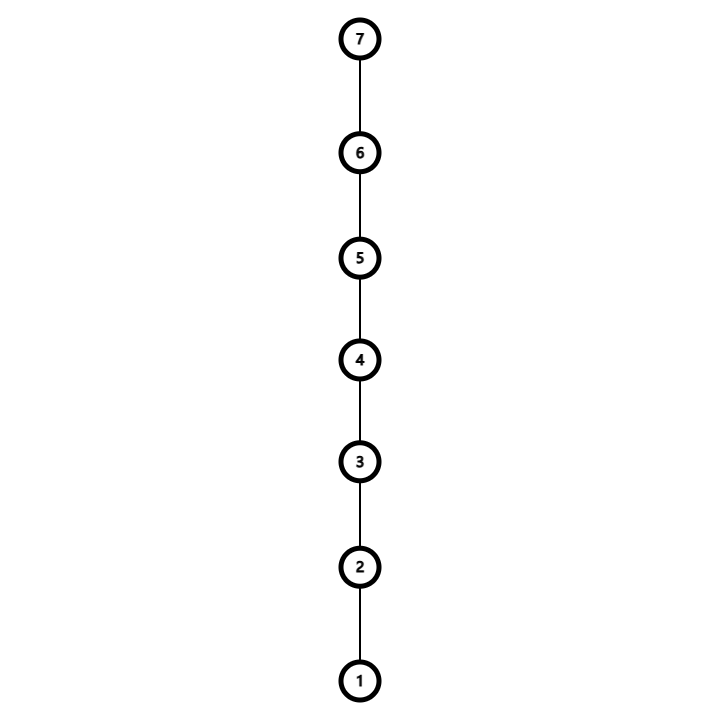
让动点 与节点 相连。显然,节点 也是叶节点。
节点 到节点 的距离为 ,节点 到节点 的距离为 ,所以节点 到节点 的距离刚好为 。
通过调整节点 的编号,即可得到距离为 的两个叶节点。
参考代码
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin>>T;
while(T--)
{
int n,q;
cin>>n>>q;
for(int i=1;i<n-1;i++)cout<<i<<' '<<i+1<<'\n';
cout<<n<<' '<<2<<'\n';
int now=2;
while(q--)
{
int d;
cin>>d;
if(d==now)cout<<-1<<' '<<-1<<' '<<-1<<'\n';
else cout<<n<<' '<<now<<' '<<d<<'\n';
now=d;
}
}
return 0;
}