P9416 [POI 2021/2022 R1] Domino
· 3 min read



解题思路
考虑使用 (横向)或 (纵向)的方块覆盖 矩形的所有格子。
如图,有两种填充方式:一个纵向方块或两个横向方块。
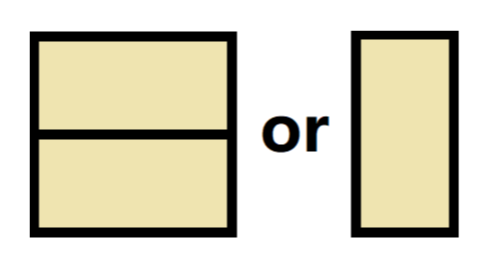
若某列中,上下两行的填充方式不一致,会导致两侧剩余奇数个格子,无法完全填满。
这两种填充方式分别覆盖了 列和 列,如果要覆盖 列,易得方案数为 Fibonacci 数列中第 项 。
我们可以占用若干列格子(障碍),将整个矩形划分为若干个矩形部分。根据乘法原理,总方案数 等于每部分方案数的乘积。
为什么 最小时,障碍一定将序列分割成若干部分:如果障碍不分割为若干部分,那么在某个连通部分中必然能找到一对孤立障碍。由于它们外侧格子数量为偶数,因此同一列的另一个格子只能向内侧覆盖,下一列的另一个格子也只能向内侧覆盖……依此类推,两个孤立障碍之间别无选择,等价于直接删除这一段。
原问题等价为:将正整数 分解为若干个 的乘积,求 的最小值(分割每个部分需要一列障碍,但最后一个不需要)。
由于 ,可以加上剪枝优化后暴力枚举。
参考代码
#include <bits/stdc++.h>
using namespace std;
using ll=long long;
const ll inf=0x3f3f3f3f3f3f3f3f;
const int N=90;
ll f[N],ans=inf;
void init()
{
f[0]=f[1]=1;
for(int i=2;i<N;i++)f[i]=f[i-1]+f[i-2];
}
void dfs(ll x,ll s)
{
if(x<=1)
{
ans=min(ans,s);
return;
}
if(ans<s)return;
for(int i=2;i<N;i++)
{
if(x%f[i])continue;
ll u=x,v=s;
while(u%f[i]==0)
{
u/=f[i];
v+=i+1;
}
dfs(u,v);
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
init();
ll m;
cin>>m;
dfs(m,0);
if(m==1)cout<<1<<'\n';
else if(ans==inf)cout<<"NIE"<<'\n';
else cout<<ans-1<<'\n';
return 0;
}