CF1899D Yarik and Musical Notes
· 2 min read



题意简述
求数列 中有多少对 (),设 ,满足 。
解题思路
作出 的图像:
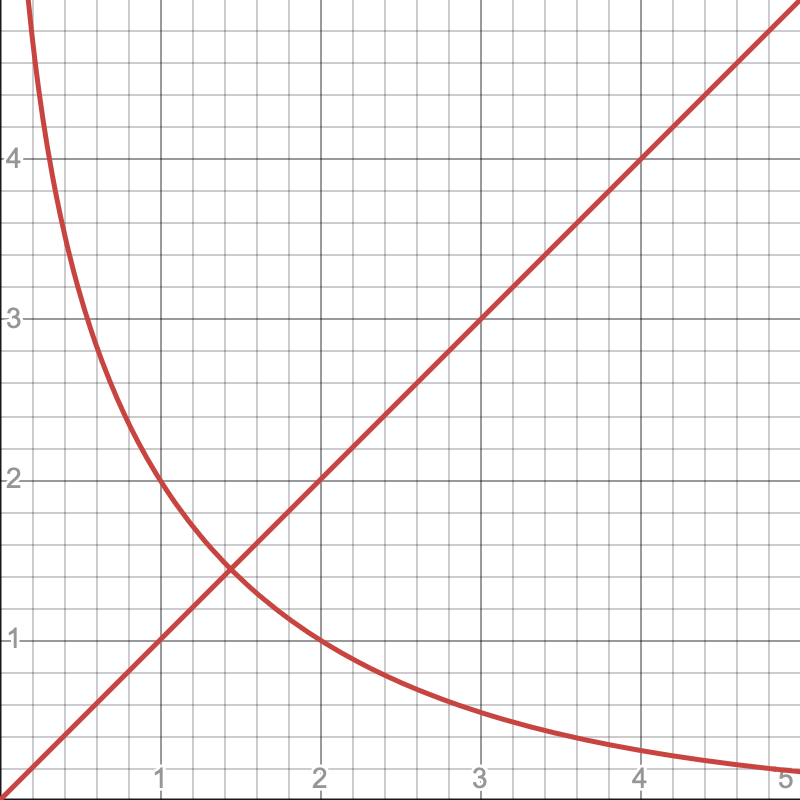
不难发现只有 或 ()时等式成立。
统计每个元素 的出现次数 ,然后对 分类讨论:
- ,选一个 和一个 ,方案数为 ;
- ,在所有的 中选两个,方案数为 。
因此总方案数为:
参考代码
#include <bits/stdc++.h>
using namespace std;
using ll=long long;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin>>T;
while(T--)
{
int n;
cin>>n;
map<int,ll> m;
for(int i=1;i<=n;i++)
{
int t;
cin>>t;
m[t]++;
}
ll ans=m[1]*m[2];
for(auto [x,y]:m)ans+=y*(y-1)/2;
cout<<ans<<'\n';
}
return 0;
}