跳到主要内容

题解：P6307 「Wdsr-1」贤者之石

· 阅读需 3 分钟
lailai
lailai
Blogger

原题链接​

参考资料​

解题思路​

定义点阵的大小为正三角形底边点的个数，即边长 +1+1。

令 ana_n 表示大小为 nn 的点阵包含的总点数，可以通过组合公式得出：

an=n(n+1)2a_n=\frac{n(n+1)}{2}

在大小为 kk 的点阵中，任意选取 33 个点的总方案数为 Cak3C_{a_k}^3。

如图所示，考虑大小为 ii 的正三角形框（图中为 i=7i=7）：

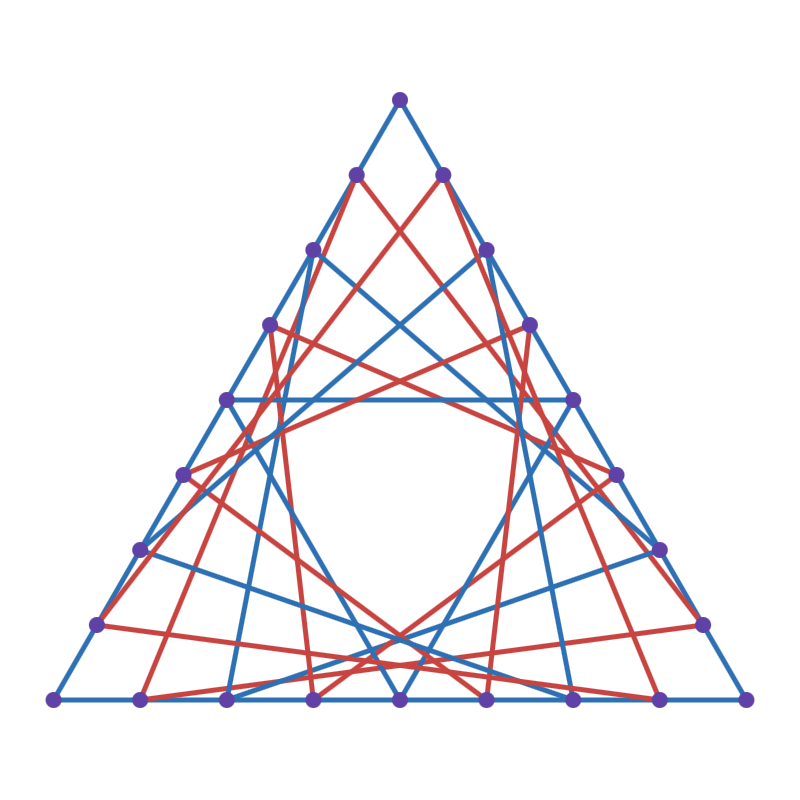
在这种大小为 ii 的三角形框中，三边对应位置的任意三个点可以构成一个正三角形。因此，每个大小为 ii 的三角形框包含 i−1i-1 个正三角形。

对于大小为 ii 的三角形框，其顶点可以位于大小为 k−i+1k-i+1 的点阵中，这样的点阵包含 ak−i+1a_{k-i+1} 个顶点。因此，每个大小为 ii 的三角形框总共有 ak−i+1a_{k-i+1} 个位置可以被选取。

因此：

Pk=∑i=1k(i−1)ak−i+1Cak3=∑i=1k(i−1)(k−i+1)(k−i+2)⋅12k(k+1)2(k(k+1)2−1)(k(k+1)2−2)⋅16=24∑i=1k(i−1)(k−i+1)(k−i+2)k(k+1)(k(k+1)−2)(k(k+1)−4)=24(−k3−3k2−2k+∑i=1ki3−(2k+4)∑i=1ki2+(k2+5k+5)∑i=1kik(k+1)(k2+k−2)(k2+k−4)=2(k4+2k3−k2−2k)(k4+2k3−k2−2k)(k2+k−4)=2k2+k−4\begin{aligned} P_k &= \frac{\sum_{i=1}^{k}(i-1)a_{k-i+1}}{C_{a_k}^{3}} \\ &= \frac{\sum_{i=1}^{k}(i-1)(k-i+1)(k-i+2)\cdot \frac{1}{2}}{\frac{k(k+1)}{2}(\frac{k(k+1)}{2}-1)(\frac{k(k+1)}{2}-2)\cdot\frac{1}{6}} \\ &= \frac{24\sum_{i=1}^{k}(i-1)(k-i+1)(k-i+2)}{k(k+1)(k(k+1)-2)(k(k+1)-4)} \\ &= \frac{24(-k^3-3k^2-2k+\sum_{i=1}^{k}i^3-(2k+4)\sum_{i=1}^{k}i^2+(k^2+5k+5)\sum_{i=1}^{k}i}{k(k+1)(k^2+k-2)(k^2+k-4)} \\ &= \frac{2(k^4+2k^3-k^2-2k)}{(k^4+2k^3-k^2-2k)(k^2+k-4)} \\ &= \frac{2}{k^2+k-4} \end{aligned}

令 r1,r2r_1,r_2 为 k2+k−4k^2+k-4 的两个根：

r1=−1+172,r2=−1−172r_1=\frac{-1+\sqrt{17}}{2},r_2=\frac{-1-\sqrt{17}}{2}

则：

∑k=m∞Pk=∑k=m∞2k2+k−4=∑k=m∞2(k−r1)(k−r2)=217∑k=m∞(1k−r1−1k−r2)=217lim⁡n→∞(∑k=mn1k−r1−∑k=mn1k−r2)=217lim⁡n→∞((ψ(n−r1+1)−ψ(m−r1))−(ψ(n−r2+1)−ψ(m−r2)))=217(ψ(m−r2)−ψ(m−r1)+lim⁡n→∞(ψ(n−r1+1)−ψ(n−r2+1)))=217(ψ(m−r2)−ψ(m−r1)+lim⁡n→∞((ψ(1)+∑k=1n−r11k)−(ψ(1)+∑k=1n−r21k)))=217(ψ(m−r2)−ψ(m−r1)+lim⁡n→∞∑k=n−r2+1n−r11k)=217(ψ(m−r2)−ψ(m−r1)+0)=217(ψ(m−−1−172)−ψ(m−−1+172))=217(ψ(m+1+172)−ψ(m+1−172))\begin{aligned} \sum_{k=m}^{\infty}P_k &= \sum_{k=m}^{\infty}\frac{2}{k^2+k-4} \\ &= \sum_{k=m}^{\infty}\frac{2}{(k-r_1)(k-r_2)} \\ &= \frac{2}{\sqrt{17}}\sum_{k=m}^{\infty}\left(\frac{1}{k-r_1}-\frac{1}{k-r_2}\right) \\ &= \frac{2}{\sqrt{17}}\lim_{n\to\infty}\left(\sum_{k=m}^{n}\frac{1}{k-r_1}-\sum_{k=m}^{n}\frac{1}{k-r_2}\right) \\ &= \frac{2}{\sqrt{17}}\lim_{n\to\infty}\left((\psi(n-r_1+1)-\psi(m-r_1))-(\psi(n-r_2+1)-\psi(m-r_2))\right) \\ &= \frac{2}{\sqrt{17}}\left(\psi(m-r_2)-\psi(m-r_1)+\lim_{n\to\infty}\left(\psi(n-r_1+1)-\psi(n-r_2+1)\right)\right) \\ &= \frac{2}{\sqrt{17}}\left(\psi(m-r_2)-\psi(m-r_1)+\lim_{n\to\infty}\left(\left(\psi(1)+\sum_{k=1}^{n-r_1}\frac{1}{k}\right)-\left(\psi(1)+\sum_{k=1}^{n-r_2}\frac{1}{k}\right)\right)\right) \\ &= \frac{2}{\sqrt{17}}\left(\psi(m-r_2)-\psi(m-r_1)+\lim_{n\to\infty}\sum_{k=n-r_2+1}^{n-r_1}\frac{1}{k}\right) \\ &= \frac{2}{\sqrt{17}}\left(\psi(m-r_2)-\psi(m-r_1)+0\right) \\ &= \frac{2}{\sqrt{17}}\left(\psi\left(m-\frac{-1-\sqrt{17}}{2}\right)-\psi\left(m-\frac{-1+\sqrt{17}}{2}\right)\right) \\ &= \frac{2}{\sqrt{17}}\left(\psi\left(m+\frac{1+\sqrt{17}}{2}\right)-\psi\left(m+\frac{1-\sqrt{17}}{2}\right)\right) \\ \end{aligned}

其中 ψ(x)\psi(x) 是 Digamma 函数，其定义为：

ψ(x)=ddxln⁡Γ(x)=Γ′(x)Γ(x)\psi(x)=\frac{\mathrm{d}}{\mathrm{d}x}\ln\Gamma(x)=\frac{\Gamma'(x)}{\Gamma(x)}

Digamma 函数满足以下递推关系：

ψ(x+1)=ψ(x)+1x\psi(x+1)=\psi(x)+\frac{1}{x}

ψ(x)\psi(x) 也可以用伯努利数 B2kB_{2k} 表示为：

ψ(x)=ln⁡(x)−12x−∑k=1∞B2k2k⋅x2k\psi(x)=\ln(x)-\frac{1}{2x}-\sum_{k=1}^{\infty}\frac{B_{2k}}{2k\cdot x^{2k}}

当 x≫1x \gg 1 时，Digamma 函数可以用渐近展开式近似为：

ψ(x)=ln⁡(x)−12x−112x2+1120x4+o(x−4)\psi(x)=\ln(x)-\frac{1}{2x}-\frac{1}{12x^2}+\frac{1}{120x^4}+o(x^{-4})

在 xx 较小时，可以通过递推关系放大。用渐进展开式求近似值。

参考代码​

#include <bits/stdc++.h>
using namespace std;

double digamma(double x)
{
	double res=0;
	while(x<10){res-=1/x;x++;}
	res+=log(x)-1/(x*2)-1/(x*x*12)+1/(x*x*x*x*120);
	return res;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	int m;
	cin>>m;
	if(m==1)
	{
		cout<<"1.7984x10^0"<<'\n';
		return 0;
	}
	double r1=(1.0-sqrt(17))/2,r2=(1.0+sqrt(17))/2;
	double ans=(digamma(m+r1)-digamma(m+r2))*(-2)/sqrt(17);
	int cnt=0;
	while(ans<1){cnt--;ans*=10;}
	cout<<fixed<<setprecision(4)<<ans<<"x10^"<<cnt<<'\n';
	return 0;
}