衔接

本章是初高衔接，补充一些初中可能没讲，但高中默认掌握的知识。

参考资料

• 乘法公式 - 维基百科
• 因式分解 - 维基百科
• 韦达定理 - 维基百科

乘法公式

平方公式

在初中阶段，我们学过的 $3$ 个 平方公式：

1. 平方差公式

$$a^2-b^2=(a+b)(a-b)$$

2. 完全平方和公式

$$(a+b)^2=a^2+2ab+b^2$$

3. 完全平方差公式

$$(a-b)^2=a^2-2ab+b^2$$

立方公式

我们将 完全平方和公式 中的平方修改为 立方，得到：

1. 完全立方和公式

$$\begin{aligned} (a+b)^3 &= (a+b)(a+b)(a+b) \\ &= (a^2+2ab+b^2)(a+b) \\ &= a^3+2a^2b+ab^2+a^2b+2ab^2+b^3 \\ &= a^3+3a^2b+3ab^2+b^3 \end{aligned}$$

同理，将 完全平方差公式 中的平方修改为 立方，得到：

2. 完全立方差公式

$$\begin{aligned} (a-b)^3 &= (a-b)(a-b)(a-b) \\ &= (a^2-2ab+b^2)(a-b) \\ &= a^3-2a^2b+ab^2-a^2b+2ab^2-b^3 \\ &= a^3-3a^2b+3ab^2-b^3 \end{aligned}$$

将 完全立方和公式 移项，并提取公因式，得到：

3. 立方和公式

$$\begin{aligned} a^3+b^3 &= (a+b)^3-3a^2b-3ab^2 \\ &= (a+b)^3-3ab(a+b) \\ &= (a+b)((a+b)^2-3ab) \\ &= (a+b)(a^2-ab+b^2) \end{aligned}$$

同理，将 完全立方差公式 移项，并提取公因式，得到：

4. 立方差公式

$$\begin{aligned} a^3-b^3 &= (a-b)^3+3a^2b-3ab^2 \\ &= (a-b)^3+3ab(a-b) \\ &= (a-b)((a-b)^2+3ab) \\ &= (a-b)(a^2+ab+b^2) \end{aligned}$$

这就是高中阶段常用的 $4$ 个 立方公式：

$$(a+b)^3=a^3+3a^2b+3ab^2+b^3$$ $$(a-b)^3=a^3-3a^2b+3ab^2-b^3$$ $$a^3+b^3=(a+b)(a^2-ab+b^2)$$ $$a^3-b^3=(a-b)(a^2+ab+b^2)$$

Example

Example 1

计算 $(x+1)^3$。

$$(x+1)^3=x^3+3x^2+3x+1$$

Example 2

计算 $(2x-3y)^3$。

$$\begin{aligned} (2x-3y)^3 &= (2x)^3+(2x)^2(-3y)+(2x)(-3y)^2+(-3y)^3 \\ &= 8x^3-36x^2y+54xy^2-27y^3 \end{aligned}$$

因式分解

因式分解 是将一个 多项式 拆分为多个 因式 相乘的过程。

公式法

我们可以将多项式每一项凑成上文中 乘法公式 的形式。

Example

Example 1

分解因式 $x^4-1$。

$$\begin{aligned} x^4-1 &= (x^2)^2-1^2 \\ &= (x^2+1)(x^2-1) \\ &= (x^2+1)(x+1)(x-1) \end{aligned}$$

Example 2

分解因式 $x^2+4y^2+4xy$。

$$\begin{aligned} x^2+4y^2+4xy &= x^2+(2y)^2+2x(2y) \\ &= (x+2y)^2 \end{aligned}$$

十字相乘法

如果要因式分解一个 二次多项式：

$$Ax^2+Bx+C$$

可以设：

$$Ax^2+Bx+C=(ax+b)(cx+d)=acx^2+(ad+bc)x+bd$$

此时要想办法凑出 $a,b,c,d$。

我们可以将 $A$ 拆分为 $ac$，$C$ 拆分为 $bd$：

$$A=ac,C=bd$$

使其 十字相乘 后等于 $B$：

$$B=ad+bc$$ $$\begin{array}{c} a \\ c \end{array} \times \begin{array}{c} b \\ d \end{array}$$

Example

Example 1

分解因式 $x^2-x-6$。

$$\begin{array}{c} 1 \\ 1 \end{array} \times \begin{array}{c} 2 \\ -3 \end{array}$$

因此 $x^2-x-6=(x+2)(x-3)$。

Example 2

分解因式 $2x^2+9x-5$。

$$\begin{array}{c} 1 \\ 2 \end{array} \times \begin{array}{c} 5 \\ -1 \end{array}$$

因此 $2x^2+9x-5=(x+5)(2x-1)$。

Example 3

分解因式 $6x^2+7x-3$。

$$\begin{array}{c} 2 \\ 3 \end{array} \times \begin{array}{c} 3 \\ -1 \end{array}$$

因此 $6x^2+7x-3=(2x+3)(3x-1)$。

Example 4

分解因式 $x^2+(3-a)-3a$。

$$\begin{array}{c} 1 \\ 1 \end{array} \times \begin{array}{c} 3 \\ -a \end{array}$$

因此 $x^2+(3-a)-3a=(x+3)(x-a)$。

Example 5

分解因式 $x^2-2y^2+xy+x+5y-2$。

$$\begin{array}{c} 1 \\ 1 \end{array} \times \begin{array}{c} 2y-1 \\ 2-y \end{array}$$

因此 $x^2-2y^2+xy+x+5y-2=(x+2y-1)(x+2-y)$。

长除法

在解 高次多项式 方程时，如果已经找到一个根，就可以把多项式拆成更简单的形式。

这样可以降低次数，方便继续求解：

1. 先找到多项式方程 $f(x)=0$ 的一个根 $a$。（瞪眼法：注意到…… 猜根法：尝试代入一些数，看结果是否为 $0$）
2. 根据 因式定理，如果 $f(a)=0$，那么 $(x-a)$ 就是 $f(x)$ 的一个因式。
3. 将 $f(x)$ 除以 $(x-a)$，得到一个新的多项式 $g(x)$，此时 $f(x)=(x-a)g(x)$。
4. 而 $g(x)$ 的次数比 $f(x)$ 低 $1$，继续分解会更简单。

与整数的除法相似，多项式可以使用 长除法。

Example

Example 1

分解因式 $x^3+2x^2-4x+1$。

注意到 $x=1$ 是方程的一个根：

$$\frac{x^3+2x^2-4x+1}{x-1}=x^2+3x-1$$

因此 $x^3+2x^2-4x+1=(x-1)(x^2+3x-1)$。

Example 2

分解因式 $x^3+x^2-3x-2$。

注意到 $x=-2$ 是方程的一个根：

$$\frac{x^3+x^2-3x-2}{x+2}=x^2-x-1$$

因此 $x^3+x^2-3x-2=(x+2)(x^2-x-1)$。

二重根式

利用等式变形方法（乘法公式 和 因式分解），可以化简 二重根式（嵌套根式）。

一般的二重根式的形式如下：

$$\sqrt{a\pm\sqrt b}$$

引入

在解数学题时，有时会遇到结果为二重根式的情况。

例如，在一个锐角为 $15\degree$ 的直角三角形中，两条直角边 $AB$ 和 $AC$ 分别为 $2+\sqrt 3$ 和 $1$。

计算斜边 $BC$ 的长度，可以用 勾股定理 推导：

$$BC=\sqrt{AB^2+AC^2}=\sqrt{(2+\sqrt 3)^2+1^2}=\sqrt{8+4\sqrt 3}$$

但这还不是最简答案，需要进一步简化。

推导

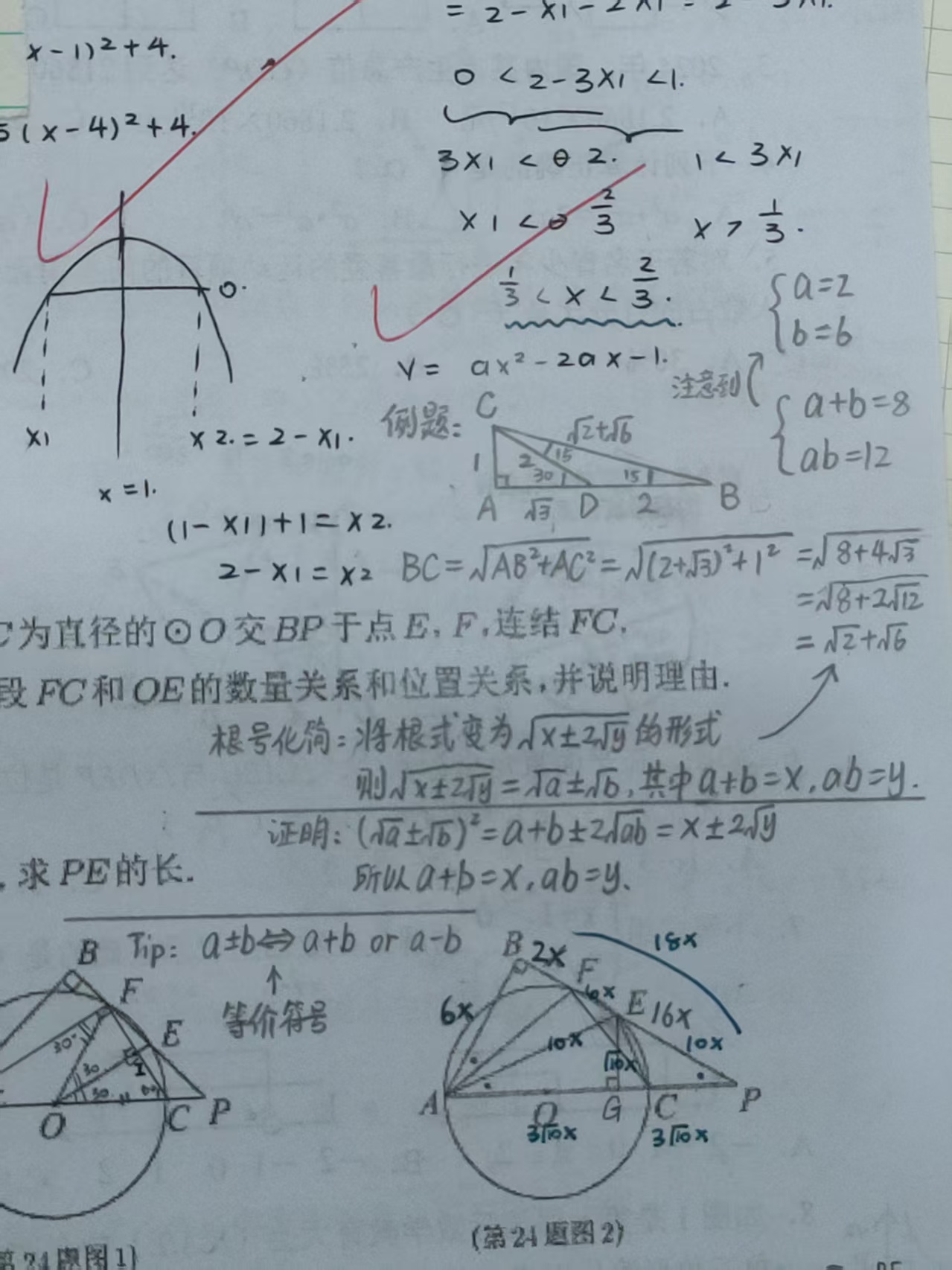
我们将化简结果设为：

$$\sqrt{8+4\sqrt{3}}=\sqrt{x}+\sqrt{y}$$

则有：

$$8+4\sqrt{3}=(\sqrt{x}+\sqrt{y})^2=x+y+2\sqrt{xy}$$

可以令：

$$x+y=8$$ $$2\sqrt{xy}=4\sqrt{3}$$

注意到一组正整数解：

$$x=2,y=6$$

因此化简结果为：

$$\sqrt{8+4\sqrt{3}}=\sqrt{2}+\sqrt{6}$$

总结

对于一般的二重根式：

$$\sqrt{a\pm\sqrt{b}}$$

我们需要找到一组正整数 $x$ 和 $y$，使得：

$$x+y=a,xy=\frac{b}{4}$$

这样就可以化简为：

$$\sqrt{a\pm\sqrt{b}}=\left|\sqrt{x}\pm\sqrt{y}\right|$$

提示

并非所有的二重根式都可以化简。

Example

Example 1

化简 $\sqrt{5-2\sqrt{6}}$。

$$\sqrt{5-2\sqrt{6}}=\left|\sqrt{2}-\sqrt{3}\right|=\sqrt{3}-\sqrt{2}$$

Example 2

化简 $\sqrt{4-\sqrt{15}}$。

$$\begin{aligned} \sqrt{4-\sqrt{15}} &= \frac{\sqrt{8-2\sqrt{15}}}{\sqrt{2}} \\ &= \left|\sqrt{5}-\sqrt{3}\right|\cdot\frac{\sqrt{2}}{2} \\ &= \frac{\sqrt{10}-\sqrt 6}{2} \end{aligned}$$

韦达定理

韦达定理 描述了 多项式方程 的 根 与 系数 之间的关系。

设一元二次方程 $ax^2+bx+c=0$ 的两根为 $x_1$ 和 $x_2$，则由：

$$ax^2+bx+c=a(x-x_1)(x-x_2)=ax^2-a(x_1+x_2)x+ax_1x_2$$

得出：

$$b=-a(x_1+x_2),c=ax_1x_2$$

移项：

$$x_1+x_2=-\frac{b}{a},x_1x_2=\frac{c}{a}$$

符号

正负号 & 负正号

正负号 $\pm$ 可以表示 近似值的精确度 或 两个可能的数值。

在生活中，食品包装袋上写着 $230\mathrm{g}\pm 10\%$，表示近似值介于 $207\mathrm{g}$ 和 $253\mathrm{g}$ 之间。

在数学中，正负号更常用于表示两个可能的数值。例如：

$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$ $$(a\pm b)^2=a^2\pm 2ab+b^2$$

正负号 $\pm$ 也可以配合 负正号 $\mp$ 使用，注意符号上下的对应顺序。例如：

$$a^3\pm b^3=(a\pm b)(a^2\mp ab+b^2)$$

连加记号 & 连乘记号

在数学中，经常遇到 $n$ 个数累加的式子：

$$a_1+a_2+\dots+a_n$$

而上述式子可以简写为：

$$\sum_{i=1}^n a_i$$

其中，$\sum$ 表示 连加记号（求和记号），$a_i$ 表示 一般项。

$i=1$ 和 $n$ 表示变量 $i$ 从 下界 $1$ 开始，每次加 $1$ 直到 上界 $n$。

Example

$$\sum_{i=3}^6 i^2=3^2+4^2+5^2+6^2=86$$

而 $\prod$ 表示 连乘记号（求积符号），用法与 连加记号 类似。

$$\prod_{i=1}^n a_i=a_1\times a_2\times\dots\times a_n$$

Example

$$\prod_{i=2}^4 2i=4\times 6\times 8=192$$

提示

连加记号 $\sum$ 是大写希腊字母 $\Sigma$（Sigma，西格玛），连乘记号 $\prod$ 是大写希腊字母 $\Pi$（Pi，派）。

根式

共轭根式

以下两个根式 $x$ 和 $y$ 互为 共轭根式：

$$x=\sqrt a+\sqrt b\iff y=\sqrt a-\sqrt b$$

不难发现它们的乘积不含根式：

$$xy=\left(\sqrt a-\sqrt b\right)\left(\sqrt a+\sqrt b\right)=a-b$$

提示

轭（è）本意指两头牛背上的架子称为轭，轭使两头牛同步行走。

共轭即为按一定的规律相配的一对，在数学中有共轭根式、共轭复数、共轭矩阵、共轭点等概念。

分母有理化

当 分母 含有根式时，同时乘以分母的 共轭根式，即可实现 分母有理化：

$$\frac{1}{\sqrt{a}}=\frac{\sqrt{a}}{\sqrt{a}\times\sqrt{a}}=\frac{\sqrt{a}}{a}$$ $$\frac{1}{\sqrt{a}-\sqrt{b}}=\frac{\sqrt{a}+\sqrt{b}}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\frac{\sqrt{a}+\sqrt{b}}{a-b}$$ $$\frac{1}{a+\sqrt{b}}=\frac{a-\sqrt{b}}{\left(a+\sqrt{b}\right)\left(a-\sqrt{b}\right)}=\frac{a-\sqrt{b}}{a^2-b}$$ $$\frac{1}{a-\sqrt{b}}=\frac{a+\sqrt{b}}{\left(a-\sqrt{b}\right)\left(a+\sqrt{b}\right)}=\frac{a+\sqrt{b}}{a^2-b}$$

思想

符号 & 单位

带 符号 的量在数学、科学，甚至生活中都很常见。

许多看似「只有大小」的量，其实也可以引入正负，用以表示方向或性质。

例如角度、面积、长度、位移、海拔、温度、记账等。

带符号有一个明显的优势：可以直接代入公式，自动处理方向和性质，简化计算与判断。

其实这个思想在初中就有了，例如选择题中类似「如果向东走 $20$ 米记作 $+20$，那么向西走 $30$ 米可以记作什么？」的问题。

Example

海拔

一个人从海拔 $0$ 米出发，连续经过以下高度变化：

上升 $300$ 米；下降 $120$ 米；上升 $50$ 米；下降 $80$ 米；下降 $100$ 米；上升 $60$ 米。

如果不用正负号，每一步都要先判断方向，再决定加减，过程繁琐。

但如果用正负数来表示（上升为正，下降为负），变成：

$$(+300)+(-120)+(+50)+(-80)+(-100)+(+60)=110$$

这样，只需把这些数值直接相加，就能快速算出最终高度。

记账

一个人从余额 $0$ 元开始，连续经过以下收支变化：

收入 $300$ 元；支出 $120$ 元；收入 $50$ 元；支出 $80$ 元；支出 $100$ 元；收入 $60$ 元。

如果不用正负号，每一步都要先判断性质，再决定加减，过程繁琐。

但如果用正负数来表示（收入为正，支出为负），变成：

$$(+300)+(-120)+(+50)+(-80)+(-100)+(+60)=110$$

这样，只需把这些数值直接相加，就能快速算出最终余额。

角度

一个机器人从正前方（$0^\circ$）开始，连续经过以下旋转变化：

左转 $300^\circ$；右转 $120^\circ$；左转 $50^\circ$；右转 $80^\circ$；右转 $100^\circ$；左转 $60^\circ$。

如果不用正负号，每一步都要先判断方向，再决定加减，过程繁琐。

但如果用正负角度表示（左转为正，右转为负），变成：

$$(+300)+(-120)+(+50)+(-80)+(-100)+(+60)=110$$

这样，只需把这些角度直接相加，就能快速算出最终方向。

与带符号运算类似，许多情况下也可以带 单位 运算。

举个极端的例子：澳大利亚的陆地面积略大于 十万公吨光年每毫米汞柱每年每三十秒。

$$\begin{aligned} S_{\text{Australia}} &= 7.6923×10^6\mathrm{km^2} \\ &> 10^5\times\mathrm{t}\cdot\mathrm{ly}/\mathrm{mmHg}/\mathrm{year}/30\mathrm{s} \\ &= 10^5\times\frac{1000\mathrm{kg}\cdot 9.4607\times 10^{15}\mathrm{m}}{133.322387415\mathrm{Pa}\cdot 31556926\mathrm{s}\cdot 30\mathrm{s}} \\ &= 10^5\times\frac{1000\times 9.4607\times 10^{15}}{133.322387415\times 31556926\times 30}\times\frac{\mathrm{kg}\cdot\mathrm{m}}{\mathrm{Pa}\cdot\mathrm{s}\cdot\mathrm{s}} \\ &= 10^5\times\frac{9.4607\times 10^{18}}{1.2617\times 10^{11}}\times\frac{\mathrm{kg}\cdot\mathrm{m}}{\mathrm{N}\cdot\mathrm{m^{-2}}\cdot\mathrm{s}\cdot\mathrm{s}} \\ &= 10^5\times 7.4983\times 10^7\times\frac{\mathrm{kg}\cdot\mathrm{m}}{\mathrm{kg}\cdot\mathrm{m}\cdot\mathrm{s^{-2}}\cdot\mathrm{m^{-2}}\cdot\mathrm{s}\cdot\mathrm{s}} \\ &= 7.4983\times 10^{12}\mathrm{m^2} \\ &= 7.4983\times 10^6\mathrm{km^2} \end{aligned}$$

增量 & 变化量

增量（Increment）指变量或函数在变化过程中所取的 改变量，通常用 $\Delta$ 表示。

例如 $x$ 的增量记为 $\Delta x$，$f(x)$ 的增量记为 $\Delta f(x)$。

变化量（Change）指量在初末两个状态之间的 差值，反映最终结果，与中间变化过程无关。

不等式

有些课程和教辅中会讲解 不等式，而高中阶段也会系统学习相关内容，因此在此一并整理。

详见 不等式。