加法原理:完成一项任务有 n 类方式,第 i 类有 ai 种方案,则完成该任务的方案数为:
i=1∑nai=a1+a2+⋯+an
从家到学校有 2 类出行方式:
- 乘地铁:可选择地铁 1 号线或 5 号线,共 2 种;
- 乘公交:可选择公交 26 路、38 路或 45 路,共 3 种。
根据加法原理,共有 2+3=5 种不同的出行方案。
乘法原理:完成一项任务有 n 个步骤,第 i 个步骤有 ai 种方案,则完成该任务的方案数为:
i=1∏nai=a1×a2×⋯×an
早上穿衣时:
- 上衣有 4 件;
- 裤子有 3 条。
根据乘法原理,共有 4×3=12 种不同的搭配方案。
全排列:将 n 个不同物品排成一列:
- 第 1 个位置有 n 种选择;
- 第 2 个位置有 n−1 种选择;
- 第 3 个位置有 n−2 种选择;
- ……
- 第 n−1 个位置有 2 种选择;
- 第 n 个位置有 1 种选择。
根据乘法原理,全排列的方案数为:
n×(n−1)×(n−2)×⋯×2×1
我们将正整数 1 到 n 的连乘积称为 阶乘,用 n 后面加感叹号(!)表示。
n×(n−1)×(n−2)×⋯×2×1=n!
特别地,我们定义:
0!=1
对于正整数 n 的阶乘,有:
n!=n×(n−1)!
0!=1,1!=1,2!=2,3!=6,4!=24,5!=120,6!=720… 考虑从 n 个不同物品中选取 m 个,排成一列:
- 第 1 个位置有 n 种选择;
- 第 2 个位置有 n−1 种选择;
- 第 3 个位置有 n−2 种选择;
- ……
- 第 m−1 个位置有 n−m+2 种选择;
- 第 m 个位置有 n−m+1 种选择。
根据乘法原理,“从 n 个不同物品中选取 m 个进行排列的方案数”的方案数为:
n×(n−1)×(n−2)×⋯×(n−m+1)=(n−m)!n!
我们用 Anm 表示 排列数:
Anm=(n−m)!n!=n×(n−1)×(n−2)×⋯×(n−m+1)
排列数还可以用 Pnm 表示,在国内高中教材中通常使用 Anm。
Anm=Pnm考虑从 n 个不同元素中选取 m 个,但不管顺序。
若考虑顺序,这就变成了排列问题,我们已经知道有 Anm 种方案。
在这些排列方案中,每组 m 个元素由于顺序不同被重复计算了 m! 次,因此真正的方案数为:
m!Anm
我们用 Cnm 表示 组合数:
Cnm=m!Anm=m!(n−m)!n!=m×(m−1)×⋯×2×1n×(n−1)×⋯×(n−m+1)
组合数还可以用 (mn) 表示,请注意 n 和 m 的位置。
Cnm=(mn)
- Cnm=Cnn−m
- Cnm=Cn−1m+Cn−1m−1
- nmCnm=Cn−1m−1
- n−mnCn−1m=Cnm
- ∑i=0nCni=Cn0+Cn1+Cn2+⋯+Cnn=2n
- Cn0+Cn2+Cn4+⋯=Cn1+Cn3+Cn5+…
- 有 n 个 完全相同 的元素,要求将其分为 k 组,保证每组至少有一个元素,一共有多少种分法?
考虑拿 k−1 块板子插入到 n 个元素两两形成的 n−1 个空里面,答案为 Cn−1k−1,本质是求 x1+x2+⋯+xk=n 的正整数解的组数。
- 若问题变换一下,每组允许为空?
考虑创造条件转化成有限制的问题一,先借 k 个元素过来,在这 n+k 个元素形成的 n+k−1 个空里面插板,答案为 Cn+k−1n,本质是求 x1+x2+⋯+xk=n 的非负整数解的组数。
- 再扩展一步,要求对于第 i 组,至少要分到 ai 个元素呢?(∑ai≤n)
本质是求 x1+x2+⋯+xk=n 的整数解的数目。
类比无限制的情况,我们借 ∑ai 个元素过来,保证第 i 组能至少分到 ai 个,也就是令 xi′=xi−ai 且 xi′≥0
得到新方程:
(x1′+a1)+(x2′+a2)+⋯+(xk′+ak)=n⟹i=1∑kxi′=n−∑ai
答案为:
Cn−∑ai+k−1k−1
-
从 n 个连续整数选 k 个,这 k 个数中两两都不相邻的组合有 Cn−k+1k 种。
-
若将 n 个 不同的 的元素分成 a 组,第 i 组的数量为 ni,其中相同的组共有 b 类,第 k 类的相同组的个数为 sk,则方案数为:
∏i=1a(ni!)×∏k=1b(sk!)n!
原理:
Cnn1Cn−n1n2…Cnana=n1!×n2!×⋯×na!n!=∏i=1a(ni!)n
将 6 本不同的书分给甲乙丙 3 人,每人 2 本,有多少种分法?
这是不同的 3 组,即没有相同的组,故不用消除组间排序,答案为:
2!2!2!6!=90如果是分成三组每组 2 本,那就要消除组间排序,答案为:
(2!2!2!)×3!6!=15将 14 个人分成人数分别为 2,2,2,4,4 的无区别的五组,有多少种分法?
(2!2!2!4!4!)(3!2!)14!=1576575二项式 是只有 2 项的多项式,例如 a+b。
在初中阶段,我们已经学过 (a+b)2 和 (a+b)3 的展开式。
考虑 (a+b)n 的各项系数有什么规律?
我们发现,(a+b)n 展开后会有 2n 项。
其中,若取 k 个因子为 a,其余 n−k 个因子为 b,就会得到含有 akbn−k 的项。
而从 n 个因子中选出 k 个为 a 的方法数正好是 Cnk。
由此,我们得到了著名的 二项式定理:
(a+b)n=k=0∑nCnkakbn−k
其中各项的系数 Cnk 叫做 二项式系数。
(2x+3y)3=8x3+36x2y+54xy2+27y3 (3x+x25)4=81x4+540x+x21350+x51500+x8625 对于三项式,也可以使用公式展开,但过程较为复杂:
(a+b+c)n=i+j+k=n∑i!j!k!n!aibjck
- Example 1
- Example 2
- Example 3
(a+b+c)3=3!0!0!3!a3+0!3!0!3!b3+0!0!3!3!c3+2!1!0!3!a2b+2!0!1!3!a2c+1!2!0!3!ab2+0!2!1!3!b2c+1!0!2!3!ac2+0!1!2!3!bc2+1!1!1!3!abc=a3+b3+c3+3a2b+3a2c+3b2a+3b2c+3c2a+3c2b+6abc 求 (x+2y−3z)6 的展开式 xy2z3 项。
1!2!3!6!x(2y)2(−3z)3=−6480xy2z3求 (x+x2−1)4 的展开式常数项。
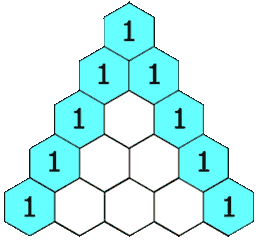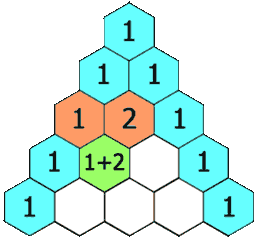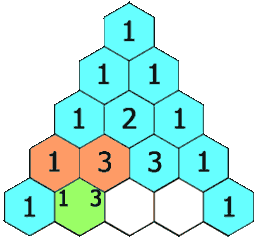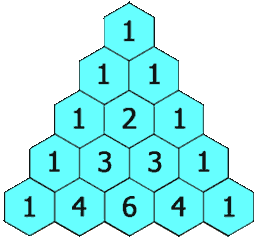
0!0!4!4!(−1)4+1!1!2!4!x⋅x2⋅(−1)2+2!2!0!4!x2⋅(x2)2=1+24+24=49我们将二项式系数排列为三角形,就得到了 杨辉三角形。

杨辉三角形中的每个数都对应一个 组合数,而每个数是它 左上方 和 右上方 的数的和。