Skip to main content

解三角形

参考资料​

约定​

对于三角形 △ABC\triangle ABC，如果没有特别说明，则：

  1. 三边长 aa、bb、cc 分别为三个角 ∠A\angle A、∠B\angle B、∠C\angle C 的对边。
  2. SS 表示三角形的 面积，s=a+b+c2s=\frac{a+b+c}{2} 表示三角形的 半周长。
  3. rr 表示 内切圆 的半径，RR 表示 外接圆 的半径。

基本方法​

基本原理​

回忆初中平几，根据全等三角形的判断：

如果知道 ASA、AAS、SAS、SSS、HL 就可以唯一的确定一个三角形。

总结一下就是两个角全都可以，三个边可以，一个角两个边就需要是夹角。

即知道 aCbaCb、cBacBa、bAcbAc，才可以唯一确定一个两边一角的三角形。

至于 SSA，只有一个角是直角才可以唯一确定，不过这个就是 HL 了。

三角形确定，意味着我们可以求出所有边的长度以及所有角度的大小。

正弦定理、余弦定理就为我们提供了方法：可以利用角度和边长互相表示。

像这样，确定三角形边、角的过程，就是解三角形。

如何选择正弦定理、余弦定理？

遇到正弦选正弦定理，遇到齐次式考虑正弦定理。

遇到余弦选余弦定理，遇到边的二次齐次式考虑余弦定理。

原则：边角统一。

三角函数​

在三角形中，

A+B+C=π\global\let\vec=\overrightarrow A+B+C=\pi

因此就有：

sin⁡A=sin⁡(B+C)sin⁡B=sin⁡(A+C)sin⁡C=sin⁡(A+B)\begin{aligned} \sin A&=\sin(B+C)\\ \sin B&=\sin(A+C)\\ \sin C&=\sin(A+B) \end{aligned} cos⁡A=−cos⁡(B+C)cos⁡B=−cos⁡(A+C)cos⁡C=−cos⁡(A+B)\begin{aligned} \cos A&=-\cos(B+C)\\ \cos B&=-\cos(A+C)\\ \cos C&=-\cos(A+B) \end{aligned} sin⁡A2=cos⁡(B+C2)sin⁡B2=cos⁡(A+C2)sin⁡C2=cos⁡(A+B2)\begin{aligned} \sin\frac{A}{2}&=\cos\left(\frac{B+C}{2}\right)\\ \sin\frac{B}{2}&=\cos\left(\frac{A+C}{2}\right)\\ \sin\frac{C}{2}&=\cos\left(\frac{A+B}{2}\right) \end{aligned} cos⁡A2=sin⁡(B+C2)cos⁡B2=sin⁡(A+C2)cos⁡C2=sin⁡(A+B2)\begin{aligned} \cos\frac{A}{2}&=\sin\left(\frac{B+C}{2}\right)\\ \cos\frac{B}{2}&=\sin\left(\frac{A+C}{2}\right)\\ \cos\frac{C}{2}&=\sin\left(\frac{A+B}{2}\right) \end{aligned}

在三角形中，a=bcos⁡C+ccos⁡Ba=b\cos C+c\cos B。

若 sin⁡2A+sin⁡2B=sin⁡2C\sin^2A+\sin^2B=\sin^2C，则该三角形是以 ∠C\angle C 为直角的 Rt△\mathrm{Rt\triangle}。

解三角形里面常用的奇怪三角函数：

sin⁡15∘=cos⁡75∘=6−24\sin15^\circ=\cos75^\circ={\sqrt6-\sqrt2\over4} sin⁡75∘=cos⁡15∘=6+24\sin75^\circ=\cos15^\circ={\sqrt6+\sqrt2\over4}

特殊的，如果 sin⁡2A=sin⁡2B\sin 2A=\sin 2B，则有 2A=2B2A=2B 或 2A+2B=π2A+2B=\pi，即 A=BA=B 或 A+B=90∘A+B=90^\circ，即等腰或直角三角形。

平面几何法​

利用平面几何定理，直接解决。

通常平面几何关注的是角与边的关系。

角，联系三角函数，倒角解决。

边，通常联系正余弦定理，以及一些特殊的定理。

建系法：将数据用坐标表示，详见解析几何。

如果直角三角形三边成等差数列，则变长一定为 3,4,53,4,5。

向量基底法​

用向量基底分解，利用点乘的性质解决。

通常情况下，向量法是一个好用而简洁的方法。

算两次原理：用同一组基底，用不同方式表示一个向量，则系数一定相等。

三角形应用​

基线：在测量过程中，根据测量的需要而确定的线段叫做基线。

仰角：在同一铅垂平面内，视线在水平线上方时与水平线的夹角。

俯角：在同一铅垂平面内，视线在水平线下方时与水平线的夹角。

方向角：从正北或正南方向到目标方向所形成的小于九十度的角。

方位角：从某点的指北方向线起依顺时针方向到目标方向线之间的水平夹角。

三角法定理​

正弦定理​

回顾初中几何，三角形面积，

S=12absin⁡C=12bcsin⁡A=12acsin⁡BS={1\over2}ab\sin C={1\over2}bc\sin A={1\over2}ac\sin B

下面的证明过程只考虑锐角三角形，对于钝角三角形，结论不变。

做过 ∠A\angle A 的垂线，则该垂线长度 hh：

h=bsin⁡C=csin⁡Bh=b\sin C=c\sin B

对每个角应用，最后可得，

asin⁡A=bsin⁡B=csin⁡C=k{a\over\sin A}={b\over\sin B}={c\over\sin C}=k

做出该三角形的外接圆，过圆心做 BCBC 的高，则，

a=2Rsin⁡A, asin⁡A=2Ra=2R\sin A,\,{a\over\sin A}=2R

即值 kk 为三角形外接圆直径 2R2R。

常常这么写：

a=2Rsin⁡A, b=2Rsin⁡B, c=2Rsin⁡Ca=2R\sin A,\,b=2R\sin B,\,c=2R\sin C sin⁡A=a2R, sin⁡B=b2R, sin⁡C=c2R\sin A={a\over2R},\,\sin B={b\over2R},\,\sin C={c\over2R}

对于任意 △ABC\triangle ABC，有：

asin⁡∠A=bsin⁡∠B=csin⁡∠C=2R\frac{a}{\sin\angle A}=\frac{b}{\sin\angle B}=\frac{c}{\sin\angle C}=2R

正弦定理推论：大边对大角，小边对小角。

余弦定理​

在 △ABC\triangle ABC 中，

AB→=CB→−CA→∣AB→∣2=∣CB→∣2+∣CA→∣2−2∣CB→∣⋅∣CA→∣⋅cos⁡θc2=a2+b2−2abcos⁡θ\begin{array}{c} \overrightarrow{AB}=\overrightarrow{CB}-\overrightarrow{CA}\\[0.5em] |\overrightarrow{AB}|^2=|\overrightarrow{CB}|^2+|\overrightarrow{CA}|^2-2|\overrightarrow{CB}|\cdot|\overrightarrow{CA}|\cdot\cos\theta\\[0.5em] c^2=a^2+b^2-2ab\cos\theta \end{array}

其中 θ\theta 为 cc 的对角，即 ∠C\angle C；第二步就是两边平方。

常写作：

cos⁡A=b2+c2−a22bc, cos⁡B=a2+c2−b22ac, cos⁡C=a2+b2−c22ab\cos A={b^2+c^2-a^2\over2bc},\,\cos B={a^2+c^2-b^2\over2ac},\,\cos C={a^2+b^2-c^2\over2ab}

对于任意 △ABC\triangle ABC，有：

a2=b2+c2−2bccos⁡Aa^2=b^2+c^2-2bc\cos A b2=a2+c2−2accos⁡Bb^2=a^2+c^2-2ac\cos B c2=a2+b2−2abcos⁡Cc^2=a^2+b^2-2ab\cos C
tip

勾股定理 实际上是 余弦定理 在一个角为 直角 时的特殊情形。

当 ∠C=90∘\angle C=90^\circ 时，有 cos⁡∠C=0\cos\angle C=0，代入余弦定理公式得到：

c2=a2+b2c^2=a^2+b^2

但直接用余弦定理证明勾股定理，可能会构成 循环论证，因为余弦定理本身可能依赖于勾股定理的成立。

推论：

a2+b2−c2>0⟹cos⁡C>0⟹C∈(0,π/2)a2+b2−c2=0⟹cos⁡C=0⟹C=π/2a2+b2−c2<0⟹cos⁡C<0⟹C∈(π/2,π)\begin{aligned} a^2+b^2-c^2>0 &\Longrightarrow \cos C>0 \Longrightarrow C\in(0,\pi/2)\\ a^2+b^2-c^2=0 &\Longrightarrow \cos C=0 \Longrightarrow C=\pi/2\\ a^2+b^2-c^2<0 &\Longrightarrow \cos C<0 \Longrightarrow C\in(\pi/2,\pi) \end{aligned}

余切定理​

ζ=1p(p−a)(p−b)(p−c)p=a+b+c2\begin{aligned} \zeta&=\sqrt{{1\over p}(p-a)(p-b)(p-c)}\\ p&={a+b+c\over2} \end{aligned}

其中 ζ\zeta 为 △ABC\triangle ABC 内切圆半径，pp 为三角形的半周长。

推论，一各三角形内切圆半径为，

R内=2Sa+b+cR_{\text{内}}={2S\over a+b+c}

其中 SS 表示三角形面积，a,b,ca,b,c 分别表示三边长。

正切定理​

正切定理指出，三角形中，两条边的和与差的比值，等于这两条边的对角的和与差的一半的正切的比值：

a−ba+b=tan⁡∠A−∠B2tan⁡∠A+∠B2{a-b\over a+b}={\tan{\angle A-\angle B\over2}\over\tan{\angle A+\angle B\over2}}

三角形四心​

编号心的名称定义
X1(I)X_1(I)内心三条 角平分线 的交点
X2(G)X_2(G)重心三条 中线 的交点
X3(O)X_3(O)外心三条 中垂线 的交点
X4(H)X_4(H)垂心三条 高线 的交点

奔驰定理​

在锐角 △ABC\triangle ABC 中，

S△BOC⋅OA→+S△AOC⋅OB→+S△AOB⋅OC→=0⃗S_{\triangle BOC}\cdot\overrightarrow{OA}+S_{\triangle AOC}\cdot\overrightarrow{OB}+S_{\triangle AOB}\cdot\overrightarrow{OC}=\vec0

推论：

  • 设 II 为内心，则 a⋅IA→+b⋅IB→+c⋅IC→=0⃗a\cdot\overrightarrow{IA}+b\cdot\overrightarrow{IB}+c\cdot\overrightarrow{IC}=\vec0.

  • 设 HH 为垂心，则 tan⁡A⋅HA→+tan⁡B⋅HB→+tan⁡C⋅HC→=0⃗\tan A\cdot\overrightarrow{HA}+\tan B\cdot\overrightarrow{HB}+\tan C\cdot\overrightarrow{HC}=\vec0.

  • 设 OO 为外心，则 sin⁡2A⋅OA→+sin⁡2B⋅OB→+sin⁡2C⋅OC→=0⃗\sin2A\cdot\overrightarrow{OA}+\sin2B\cdot\overrightarrow{OB}+\sin2C\cdot\overrightarrow{OC}=\vec0.

欧拉线定理​

  • 欧拉定理：O,IO,I 分别为外接圆、内切圆圆心，则有 OI2=R2−2RrOI^2=R^2-2Rr.

  • 欧拉线定理：三角形的外心 OO，垂心 HH，重心 GG 依次位于同一直线上，且重心到外心的距离是重心到垂心的距离的一半，即

    OG→=13OH→=13(OA→+OB→+OC→)\overrightarrow{OG}=\frac{1}{3}\overrightarrow{OH}=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})

极化恒等式​

一般形式：

  • 已知平面上非零向量 a\boldsymbol{a} 与 b\boldsymbol{b}，则 a⋅b=14(∣a+b∣2−∣a−b∣2)\boldsymbol{a} \cdot \boldsymbol{b} = \frac{1}{4}(|\boldsymbol{a} + \boldsymbol{b}|^2 - |\boldsymbol{a} - \boldsymbol{b}|^2)。

  • 在 △ABC\triangle ABC 中，若 MM 是 BCBC 的中点，则 AB→⋅AC→=∣AM→∣2−14∣BC→∣2\overrightarrow{AB} \cdot \overrightarrow{AC} = |\overrightarrow{AM}|^2 - \frac{1}{4}|\overrightarrow{BC}|^2。

在 △ABC\triangle ABC 中，对于共起点的数量积 AB→⋅AC→\overrightarrow{AB} \cdot \overrightarrow{AC} 的求解问题，我们首先想到的是找出 BCBC 的中点 MM，则

AM→=12(AB→+AC→)\overrightarrow{AM} = \frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC})

所以

AB→⋅AC→=[12(AB→+AC→)]2−14∣BC→∣2\overrightarrow{AB} \cdot \overrightarrow{AC} = \left[\frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC})\right]^2 - \frac{1}{4}|\overrightarrow{BC}|^2

化简整理便可得到如下结论：在 △ABC\triangle ABC 中，

2AB→⋅AC→=∣AB→∣2+∣AC→∣2−∣BC→∣22\overrightarrow{AB} \cdot \overrightarrow{AC} = |\overrightarrow{AB}|^2 + |\overrightarrow{AC}|^2 - |\overrightarrow{BC}|^2

任何事物都是由特殊再到一般，我们研究平面几何问题更多的是在研究三角形，因为三角形是我们接触最多也是最熟悉的，然后由三角形再延伸到四边形问题。那么对于向量余弦式是否也可以延伸到四边形呢？我们知道四边形通过对角线是可以分割成三角形的，下面一起来探讨这个问题。在平面四边形 ABCDABCD 中，它可以由 △ABC\triangle ABC 与 △ACD\triangle ACD 组成，则在 △ABC\triangle ABC 中，由向量余弦式可得

AB→⋅AC→=∣AB→∣2+∣AC→∣2−∣BC→∣22\overrightarrow{AB} \cdot \overrightarrow{AC} = \frac{|\overrightarrow{AB}|^2 + |\overrightarrow{AC}|^2 - |\overrightarrow{BC}|^2}{2}

那么在 △ACD\triangle ACD 中，则向量余弦式可得

AD→⋅AC→=∣AD→∣2+∣AC→∣2−∣DC→∣22\overrightarrow{AD} \cdot \overrightarrow{AC} = \frac{|\overrightarrow{AD}|^2 + |\overrightarrow{AC}|^2 - |\overrightarrow{DC}|^2}{2}

两式相减可得

AD→⋅AC→−AB→⋅AC→=∣AD→∣2+∣AC→∣2−∣DC→∣22−∣AB→∣2+∣AC→∣2−∣BC→∣22\overrightarrow{AD} \cdot \overrightarrow{AC} - \overrightarrow{AB} \cdot \overrightarrow{AC} = \frac{|\overrightarrow{AD}|^2 + |\overrightarrow{AC}|^2 - |\overrightarrow{DC}|^2}{2} - \frac{|\overrightarrow{AB}|^2 + |\overrightarrow{AC}|^2 - |\overrightarrow{BC}|^2}{2}

整理后可得

AC→⋅BD→=∣AD→∣2+∣BC→∣2−∣AB→∣2−∣CD→∣22\overrightarrow{AC} \cdot \overrightarrow{BD} = \frac{|\overrightarrow{AD}|^2 + |\overrightarrow{BC}|^2 - |\overrightarrow{AB}|^2 - |\overrightarrow{CD}|^2}{2}

这就得到了平面四边形的向量余弦式的形式。

在四边形 ABCDABCD 中，

AC→⋅BD→=∣AD→∣2+∣BC→∣2−∣AB→∣2−∣CD→∣22\overrightarrow{AC} \cdot \overrightarrow{BD} = \frac{|\overrightarrow{AD}|^2 + |\overrightarrow{BC}|^2 - |\overrightarrow{AB}|^2 - |\overrightarrow{CD}|^2}{2}

这个结论也称之为对角线定理，它不仅仅可以在平面四边形中得到应用，还可以推广到空间四边形的情形。

分点的向量方程​

特殊的，中点的向量方程：

AD⃗=12AB⃗+12AC⃗\vec{AD}=\frac12\vec{AB}+\frac12\vec{AC}

即对边比例相乘向量相加。

重心​

重心（Centroid）为三条 中线 的交点，又称为 形心 或 质心。

在平面直角坐标系中，重心的坐标是顶点坐标的算术平均，也就是说对于平面内任意一点 PP：

PG⃗=13(PA⃗+PB⃗+PC⃗)\vec{PG}=\frac13\left(\vec{PA}+\vec{PB}+\vec{PC}\right)

重心和三角形任意两个顶点组成的三个三角形面积相等，而重心到三条边的距离与三条边的长成反比。

根据奔驰定理，有三角形重心到其各个顶点向量之和为零。

GA⃗+GB⃗+GC⃗=0⃗\vec{GA}+\vec{GB}+\vec{GC}=\vec 0

特性：一个三角形的重心同时也是其中点三角形的重心，中位线证明。

根据是中线的性质，做 AGAG 并延长交 BCBC 于点 HH，则：

AGGH=21\frac{AG}{GH}=\frac21

特殊的，重心到三边距离之积最大、到三角形三个顶点距离的平方和最小。

内心​

内心（Incenter）为三个内角的 角平分线 的交点，即 内切圆 的圆心。

内心为三角形内切圆圆心，因此为三个角的角平分线交点：

AI⃗=λ(AB⃗∣AB⃗+AC⃗∣AC⃗∣)\vec{AI}=\lambda\left(\frac{\vec{AB}}{|\vec{AB}}+\frac{\vec{AC}}{|\vec{AC}|}\right)

有奔驰定理的形式：

sin⁡A⋅IA⃗+sin⁡B⋅IB⃗+sin⁡C⋅IC⃗=0⃗\sin A\cdot\vec{IA}+\sin B\cdot\vec{IB}+\sin C\cdot\vec{IC}=\vec 0

三角形的内心到边的距离（即内切圆的半径）与三边长及面积之间有关系：

r内=2Sa+b+c=2SCr_{\text{内}}=\frac{2S}{a+b+c}=\frac{2S}{C}

可以连接内心与三顶点，等面积法求解。

外心​

外心（Circumcenter）为三条边的 中垂线 的交点，即 外接圆 的圆心。

外心为三角形外接圆圆心，因此为三边中垂线交点，不一定在三角形内部，到三角形三点距离相等。

OA⃗2=OB⃗2=OC⃗2\vec{OA}^2=\vec{OB}^2=\vec{OC}^2

有奔驰定理的形式：

sin⁡2A⋅OA⃗+sin⁡2B⋅OB⃗+sin⁡2C⋅OC⃗=0⃗\sin2A\cdot\vec{OA}+\sin2B\cdot\vec{OB}+\sin2C\cdot\vec{OC}=\vec 0

而，

R外=abc4SR_{\text{外}}={abc\over4S}

  • 当三角形为锐角三角形时，外心在三角形内部。

  • 当三角形为钝角三角形时，外心在三角形外部。

  • 当三角形为直角三角形时，外心在斜边的中点上。

锐角三角形外心到三边距离之和等于 R+rR+r。

证明：等价于证

R(cos⁡A+cos⁡B+cos⁡C)=R+rR(\cos A+\cos B+\cos C)=R+r

我们知道

SΔABC=12(a+b+c)r=SΔOAB+SΔOAC+SΔOBC=12R(acos⁡A+bcos⁡B+ccos⁡C)\begin{aligned} S_{\Delta ABC}&=\frac{1}{2}(a+b+c)r\\ &=S_{\Delta OAB}+S_{\Delta OAC}+S_{\Delta OBC}\\ &=\frac{1}{2}R(a\cos A+b\cos B+c\cos C) \end{aligned}

联立上两式（相乘），直接展开易知等式成立。

垂心​

垂心（Orthocenter）为三条 高线 的交点。

垂心是三角形三边垂线的交点，因此有点积为零。

HA⃗⋅BC=HB⃗⋅AC⃗=HC⃗⋅AB⃗=0\vec{HA}\cdot{BC}=\vec{HB}\cdot\vec{AC}=\vec{HC}\cdot\vec{AB}=0

两两整理，得到：

HA⃗⋅HB⃗=HB⃗⋅HC⃗=HC⃗⋅HA⃗\vec{HA}\cdot\vec{HB}=\vec{HB}\cdot\vec{HC}=\vec{HC}\cdot\vec{HA}

有奔驰定理的形式：

tan⁡A⋅HA⃗+tan⁡B⋅HB⃗+tan⁡C⋅HC⃗=0⃗\tan A\cdot\vec{HA}+\tan B\cdot\vec{HB}+\tan C\cdot\vec{HC}=\vec 0

而垂心到三角形一顶点距离等于此三角形外心到此顶点对边距离的 22 倍。

三角形外心 OO、重心 GG、垂心 HH 三点共线且 OG:GH=1:2OG:GH=1:2 此直线称为三角形的欧拉线。

旁心​

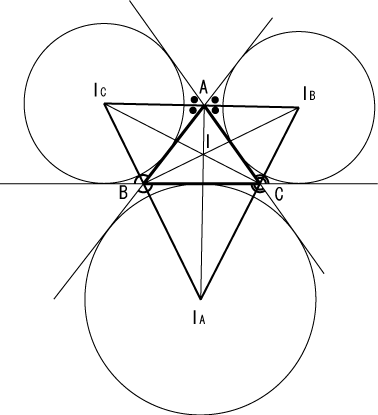
除了四心之外，三角形还有旁心。

旁心（Excenter）为外角的 角平分线 的交点，每个三角形有 33 个旁心，分别为三角形某一边的 旁切圆 的圆心。

三角形三线​

中线长定理​

在 △ABC\triangle ABC 中，BCBC 的中点为 MM，对于中线 AMAM，有：

AM2=12b2+12c2−14a2AM^2={1\over2}b^2+{1\over2}c^2-{1\over4}a^2

或，

AM2+BM2=12(AC2+AB2)AM^2+BM^2={1\over2}(AC^2+AB^2)

或，

AM=122b2+2c2−a2AM={1\over2}\sqrt{2b^2+2c^2-a^2}

证明，基底分解：

AM→=12AB→+12AC→\overrightarrow{AM}={1\over2}\overrightarrow{AB}+{1\over2}\overrightarrow{AC} BM→=12AC→−12AB→\overrightarrow{BM}={1\over2}\overrightarrow{AC}-{1\over2}\overrightarrow{AB}

则，

∣AM→∣2+∣BM→∣2=12∣AB→∣2+12∣AC→∣2|\overrightarrow{AM}|^2+|\overrightarrow{BM}|^2={1\over2}|\overrightarrow{AB}|^2+{1\over2}|\overrightarrow{AC}|^2

或者中点两个底角分别列余弦定理，相加化简。

分角定理​

在 △ABC\triangle ABC 中，BCBC 上有一点 MM，则：

BMCM=ABsin⁡∠BAMACsin⁡∠CAM{BM\over CM}={AB\sin\angle BAM\over AC\sin\angle CAM}

证明，左右两边等面积法：

BMCM=S△ABMS△ACM=AB⋅AMsin⁡∠BAMAC⋅AMsin⁡∠CAM=ABsin⁡∠BAMACsin⁡∠CAM{BM\over CM}={S_{\triangle ABM}\over S_{\triangle ACM}}={AB\cdot AM\sin\angle BAM\over AC\cdot AM\sin\angle CAM}={AB\sin\angle BAM\over AC\sin\angle CAM}

或正弦定理：

BMsin⁡∠BAM=ABsin⁡∠AMB{BM\over\sin\angle BAM}={AB\over\sin\angle AMB} CMsin⁡∠CAM=ACsin⁡∠AMC{CM\over\sin\angle CAM}={AC\over\sin\angle AMC}

上下做比。

角平分线定理​

在 △ABC\triangle ABC 中，∠A\angle A 的平分线 AMAM，有：

BMCM=ABAC{BM\over CM}={AB\over AC}

是分角定理的直接推论。

角平分线长定理​

AD=AB⋅AC−BD⋅CD=bc(1−a2(b+c)2)=2bcb+ccos⁡A2\begin{aligned} AD &= \sqrt{AB\cdot AC-BD\cdot CD} \\ & = \sqrt{bc\left(1-{a^2\over(b+c)^2}\right)} \\ & = {2bc\over b+c}\cos{A\over2} \end{aligned}

边长公式​

射影定理​

射影定理表示为：

a=bcos⁡C+ccos⁡Ba=b\cos C+c\cos B

在初中我们学习过影高乘积等于树高平方的射影定理。

在 △ABC\triangle ABC 中 BCBC 上的高为 ADAD，则：

AB2=BD⋅BCAB^2=BD\cdot BC AD2=BD⋅CDAD^2=BD\cdot CD AC2=BC⋅CDAC^2=BC\cdot CD

斯图尔特定理​

又译斯台沃特定理，在 △ABC\triangle ABC 边 BCBC 上任意一点 DD，

AB2⋅CD+AC2⋅BD−AD2⋅BC=BD⋅CD⋅BCAB^2\cdot CD+AC^2\cdot BD-AD^2\cdot BC=BD\cdot CD\cdot BC

可以由两次余弦定理推导得出。

平行四边形恒等式​

AB2+BC2+CD2+AD2=AC2+BD2AB^2+BC^2+CD^2+AD^2=AC^2+BD^2

对于一般的四边形，等式不成立，但是有不等式：

AB2+BC2+CD2+AD2≥AC2+BD2AB^2+BC^2+CD^2+AD^2\ge AC^2+BD^2

或者设 xx 表示两条对角线中点所连线段的长度：

AB2+BC2+CD2+AD2=AC2+BD2+4x2AB^2+BC^2+CD^2+AD^2=AC^2+BD^2+4x^2

注意到平行四边形对角线互相平分，即 x=0x=0，可得上面的第一个恒等式。

边元塞瓦定理​

其逆定理用于表示三角形内三点共线，角元塞瓦定理较为复杂。

梅涅劳斯定理​

一直线与 △ABC\triangle ABC 的三边 AB,BC,ACAB,BC,AC 或他们的延长线分别交于 X,Y,ZX,Y,Z 三点，则：

AXXB⋅BYYC⋅CZZA=0\frac{AX}{XB}\cdot\frac{BY}{YC}\cdot\frac{CZ}{ZA}=0

梅涅劳斯定理的逆定理表示为，满足上述式子，则 X,Y,ZX,Y,Z 三点共线。

面积公式​

基本公式（底 + 高）：

S=12aha=12bhb=12chcS=\frac{1}{2}ah_a=\frac{1}{2}bh_b=\frac{1}{2}ch_c

两边 + 夹角：

S=12abcos⁡∠C=12accos⁡∠B=12bccos⁡∠AS=\frac{1}{2}ab\cos{\angle C}=\frac{1}{2}ac\cos{\angle B}=\frac{1}{2}bc\cos{\angle A}

海伦公式（三边）：

S=s(s−a)(s−b)(s−c)S=\sqrt{s(s-a)(s-b)(s-c)}

秦九昭公式（三边）：

S=14(a2c2−(a2+c2−b22)2)S=\sqrt{\frac{1}{4}\left(a^2c^2-\left(\frac{a^2+c^2-b^2}{2}\right)^2\right)}

内切圆 + 三边：

S=sr=12r(a+b+c)S=sr=\frac{1}{2}r(a+b+c)

外接圆 + 边/角：

S=abc4R=2R2sin⁡∠Asin⁡∠Bsin⁡∠C=12R2(sin⁡∠2A+sin⁡∠2B+sin⁡∠2C)S=\frac{abc}{4R}=2R^2\sin{\angle A}\sin{\angle B}\sin{\angle C}=\frac{1}{2}R^2(\sin{\angle 2A}+\sin{\angle 2B}+\sin{\angle 2C})

三角 + 一边：

S=a2sin⁡∠Bsin⁡∠Csin⁡∠A=b2sin⁡∠Asin⁡∠Csin⁡∠B=c2sin⁡∠Asin⁡∠Bsin⁡∠CS=\frac{a^2\sin{\angle B}\sin{\angle C}}{\sin{\angle A}}=\frac{b^2\sin{\angle A}\sin{\angle C}}{\sin{\angle B}}=\frac{c^2\sin{\angle A}\sin{\angle B}}{\sin{\angle C}}

三边 + 一角：

S=14(a2+b2−c2)tan⁡∠C=14(a2+c2−b2)tan⁡∠B=14(b2+c2−a2)tan⁡∠AS=\frac{1}{4}(a^2+b^2-c^2)\tan{\angle C}=\frac{1}{4}(a^2+c^2-b^2)\tan{\angle B}=\frac{1}{4}(b^2+c^2-a^2)\tan{\angle A} S=s(s−a)tan⁡∠A2=s(s−b)tan⁡∠B2=s(s−c)tan⁡∠C2S=s(s-a)\tan{\frac{\angle A}{2}}=s(s-b)\tan{\frac{\angle B}{2}}=s(s-c)\tan{\frac{\angle C}{2}}

两边 + 两角：

S=14a2sin⁡2∠B+14b2sin⁡2∠A=14a2sin⁡2∠C+14c2sin⁡2∠A=14b2sin⁡2∠C+14c2sin⁡2∠BS=\frac{1}{4}a^2\sin{2\angle B}+\frac{1}{4}b^2\sin{2\angle A}=\frac{1}{4}a^2\sin{2\angle C}+\frac{1}{4}c^2\sin{2\angle A}=\frac{1}{4}b^2\sin{2\angle C}+\frac{1}{4}c^2\sin{2\angle B}

向量：

S=12∣AB→×AC→∣=12∣BA→×BC→∣=12∣CA→×CB→∣S=\frac{1}{2}\left|\overrightarrow{AB}\times\overrightarrow{AC}\right|=\frac{1}{2}\left|\overrightarrow{BA}\times\overrightarrow{BC}\right|=\frac{1}{2}\left|\overrightarrow{CA}\times\overrightarrow{CB}\right|

等边三角形：

S=34a2S=\frac{\sqrt 3}{4}a^2

布雷特施奈德公式​

任意四边形面积可以表示为：

S=(p−a)(p−b)(p−c)(p−d)−abcdcos⁡2α+β2p=a+b+c+d2\begin{aligned} S&=\sqrt{(p-a)(p-b)(p-c)(p-d)-abcd\cos^2{\alpha+\beta\over2}}\\ p&={a+b+c+d\over2} \end{aligned}

其中 pp 为四边形的半周长，α,β\alpha,\beta 为其中二个对角。

布雷特施奈德公式可视为婆罗摩笈多公式之推广。

婆罗摩笈多公式​

注意到圆内接四边形对角互补，其半角余弦值为零，cos⁡90∘=0\cos90^\circ=0 则圆内接四边形面积可以简化为：

S=(p−a)(p−b)(p−c)(p−d)p=a+b+c+d2\begin{aligned} S&=\sqrt{(p-a)(p-b)(p-c)(p-d)}\\ p&={a+b+c+d\over2} \end{aligned}

其中 pp 为四边形的半周长。