带有方向的线段称为有向线段。有向线段的三要素为:起点、方向、长度。
根据初等几何,那么只要知道这三要素,这个有向线段就已经被确定了,也就是终点可知。
从另一个角度思考,也可以认为是知道起点、终点,就可以唯一的确定一个有向线段。
一个有向线段由其两个端点表示,记为 AB 或 a,同时我们记其长度,称为向量的模。
向量(vector)又称欧几里得向量(Euclidean vector)。
目前没有准确而统一的中文翻译,在物理、工程中通称矢量。
一般指一个同时具有大小和方向,且满足平行四边形法则的几何对象。
向量是数学、物理学和工程科学等多个自然科学中的基本概念。
与向量相对的概念称标量、纯量、数量,即:
只有大小、绝大多数情况下没有方向(电流是特例)、不满足平行四边形法则的量。
固定向量:尤其在物理学领域,有些向量会与起点有关(力与其的作用点有关,质点运动速度与该质点的位置有关),因而假设向量有确定的起点和终点,当起点和终点改变后,构成的向量就不再是原来的向量。这样的向量也被称为固定向量。
自由向量:向量的位置可自由移动。在另一些时候,由于向量的共性都具有大小和方向,会认为向量的起点和终点并不那么重要。两个起点不一样的向量,只要大小相等,方向相同,就可以称为是同一个向量。这样的向量被称为自由向量。在数学中,一般只研究自由向量,并且数学中所指的向量就是指自由向量。也就是只要大小以及方向一样,即可视为同一向量,与向量的起始点并无关系。
特殊的向量:遇到某些特殊情况(如表示磁场的磁感应强度)需要表示与记载纸面垂直的向量,则会使用圆圈中打叉或打点的方式来表示(如右图)。圆圈中带点的记号(⊙)表示由纸下方指向纸上方的向量,而圆圈中带叉的记号(⊗)则表示由纸的上方指向纸下方的向量。由于这种记号不表示向量的大小,所以必须时需要在旁边或其它地方另外注明。
下文为高中数学中定义的向量。
无特殊说明,下文的向量均指自由向量,大部分都是平面向量。
既有大小又有方向的量称为向量。这个定义很抽象,我们逐个分解。
我们已经有了有向线段,但是实际应用中,大部分时候,向量的位置并不重要。
于是我们将有向线段的起点不固定,将一个有向线段抽象为一个可以随意移动的量。
此时,你也许发现了。有向线段其实可以再次表示为,起点和一个向量。
我们通常把向量表示在平面直角坐标系内,没有说明的情况下,起点通常标在坐标轴原点。
我们取这个向量在横、纵坐标上延伸的长度作为两个元素,将向量记为 (a,b)。
那么我们就得出了向量的几何意义,即向量 (a,b) 表示向右走 a、向上走 b 的位移。
已知两点 A(a,b),B(c,d),易证
AB=(c−a,d−b)。
对于一个向量 a,有向线段
a 的长度称为向量的模,即为这个向量的大小。
符号表示为 ∣a∣ 或 ∣AB∣ ,根据勾股定理,我们知道 ∣a∣=∣(x,y)∣=x2+y2。
零向量:模为 0 的向量,零向量的方向任意(不过其实是无意义)。一般记为:0。
单位向量:模为 1 的向量称为单位向量。一般记为 e,最常见的单位向量就是基向量。
基向量:i=(1,0) 表示 x 方向的单位向量,j=(0,1) 表示 y 方向的单位向量。
平行向量:方向相同或相反的两个非零向量,规定零向量与任何向量平行。记作: x∥y。
共线向量:任一组平行向量都可以平移到同一直线上,所以平行向量又叫共线向量。
相等向量:模相等且方向相同的向量。相反向量:模相等且方向相反的向量。
我们称 x 轴与 y 轴的角度为 θ(θ=π/2) 的坐标系。
定义平面直角坐标系中的点 P(x,y),将 P 转移到斜坐标系中变成 P′(x′,y′) 满足:
{x′=x+ycosθy′=ysinθ
⎩⎨⎧x=x′−tanθy′y=sinθy′
于是我们可以把平面向量在平面直角坐标系中的一些运算迁移到斜坐标系中:
-
数量积:(x1′,y1′)⋅(x2′,y2′)=x1x2+y1y2+(x1y2+x2y1)cosθ。
-
模长:a=(x′,y′),∣a∣=x2+y2+2xycosθ。
-
夹角:a=(x1′,y1′),b=(x2′,y2′),cosγ=∣a∣∣b∣a⋅b。
我们规定实数 λ 与向量 a 的积为一个向量,称为向量的数乘运算,记作 λa。
我们定义 λa=λ(x,y)=(λx,λy)。据此,我们可以得出以下向量数乘常用的结论:
- ∣λa∣=∣λ∣∣a∣;
- 当 λ>0 时,λa 与 a 同向;
- 当 λ=0 时,λa=0;
- 当 λ<0 时,λa 与 a 方向相反。
根据数乘的定义,可以得出向量的数乘满足交换律、结合律、分配律等,即,
λ(μa)=(λμ)a
λ(a+b)=λa+λb
(λ+μ)a=λa+μa
(−λ)a=−(λa)=λ(−a)
注意,向量的数乘本质上也属于向量的线性运算,不过我把他们分开,方便理解。
下面讨论向量的加法,类比的,向量的减法可以从公式入手理解。
类比物理中的位移,从 A 经 B 到 C,那么经过的位移等价于直接从 A 到 C。
符号表示即:AB+BC=AC,其实这个也就是三角形法则所表述的。
向量减法类似:OA−OB=OA+BO=BA,后面用到了交换律。
同时,注意到力的合成法则(平行四边形法则),同样也可以看做向量的相加。
因此,我们得出向量相加的两个运算法则,即三角形法则、平行四边形法则:
-
三角形法则:首尾顺次相连,和为从第一个向量的起点指向最后一个向量的终点;
-
平行四边形法则:向量共起点,和为以这两个向量为邻边的平行四边形的对角线,
起点为两个向量共有的起点,方向沿平行四边形对角线方向。
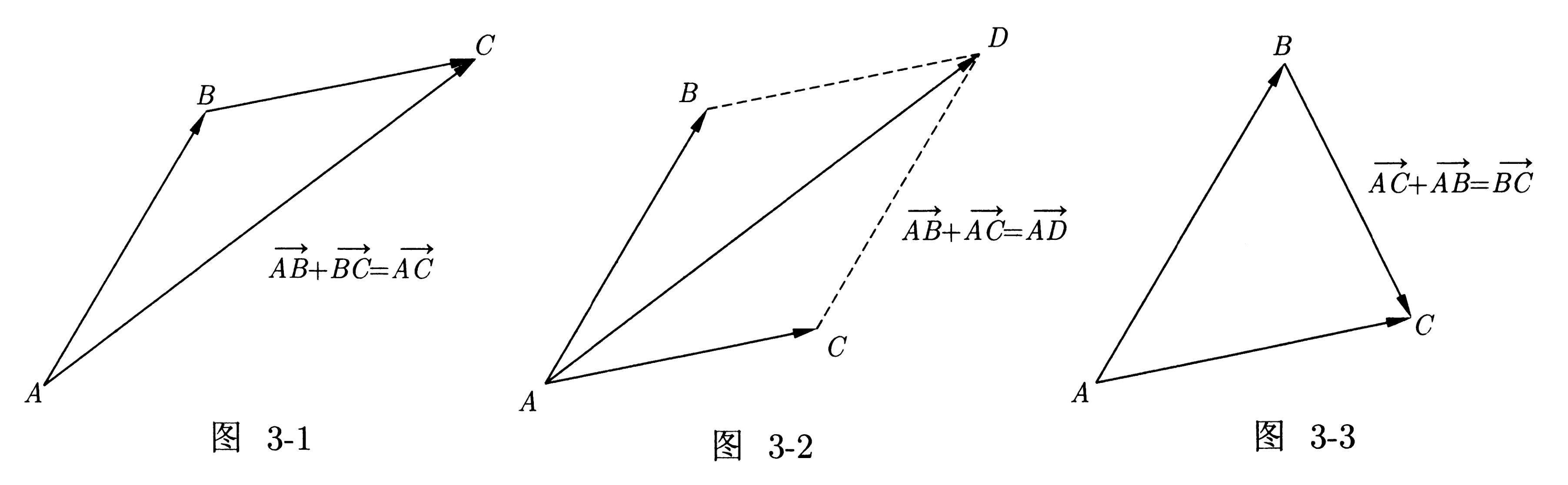
这样,向量的加法就具有了几何意义。并且向量的加法满足交换律与结合律。
然后从几何的角度可以推出一些公式,其中三角形法则的公式比较简单,如下:
(x1,y1)+(x2,y2)=(x1+x2,y1+y2)
向量加法满足结合律和交换律,画图理解即可。
向量加法可以导出三角形不等式,
∣∣a∣−∣b∣∣≤∣a+b∣≤∣a∣+∣b∣
当且仅当两向量方向相同(注意不是平行),取等。
设 A(x1,y1)、B(x2,y2) 为一平面内两点。
设 C(x,y) 为线段 AB 中点,则 AC=CB:
x−x1=x2−x
y−y1=y2−y
最终解得,
C(2x1+x2,2y1+y2)
即中点坐标。
设 A(x1,y1)、B(x2,y2) 为一平面内两点,则,
∣AB∣=AB⋅AB=(x1−x2)2+(y1−y2)2
则线段 AB,
∣AB∣=∣AB∣=(x1−x2)2+(y1−y2)2
即线段长度。
对于向量的乘法:
| 物理 | 数学 | 直译 | 俗称 |
|---|
| 标量积 | 数量积 | 内积 | 点积 |
| 矢量积 | 向量积 | 外积 | 叉积 |
物理和数学上的用语采用了意译的方法,分别表示运算的结果为标量和矢量。
在数学学科,通常也可以翻译成「内积」和「外积」,是两个名词的直译。
而「点积」和「叉积」是根据运算符号得来的俗称,这种俗称也很常见。
点积的概念对于任意维数的向量都适用。
已知两个向量 a,b ,它们的夹角为 θ,那么这两个向量的点积为:
a⋅b=∣a∣∣b∣cosθ
-
其中,我们称 ∣a∣cosθ 为 a 在 b 方向上的投影。
∣a∣cosθ=∣b∣a⋅b
而投影向量需要再乘上 b 方向的单位向量:
∣b∣2a⋅bb
-
其中,θ∈[0,π],但是直线的夹角 θ∈[0,π),因为相反向量是完全不同的。
点积的几何意义即为:点积 a⋅b 等于 a 的模与 b 在 a 方向上的投影的乘积。
另外,我们定义向量点积数值上表示为(简记为先相乘再相加):
(x1,y1)⋅(x2,y2)=x1x2+y1y2
可以发现,这种运算得到的结果是一个标量,并不属于向量的线性运算。
向量与零向量点积,结果为 0。在不引起混淆的情况下,点积的点号可以省略不写。
向量点乘满足交换律:
a⋅b=b⋅a=∣a∣⋅∣b∣⋅cosθ
向量点乘对数乘有结合律:
(λa)⋅b=λ(a⋅b)=a⋅(λb)
向量点乘对向量加法有分配率:
(a+b)⋅c=a⋅c+b⋅c
但是向量点乘不满足结合律,
(a⋅b)⋅c=a⋅(b⋅c)
注意到向量运算具有大部分的数字运算的性质(除了除法),因此可以当做字母计算。
可以得到,若 b=c,a⋅b=a⋅c 的充要条件是 a⊥(b−c),
a⋅b=a⋅c
a⋅(b−c)=0
即,
a⊥(b−c)
不难发现,
∣a+b∣2−∣a−b∣2=4a⋅b
a⋅b=41(∣a+b∣2−∣a−b∣2)
即极化恒等式,我们可以不通过求夹角的方式得出两向量点积。
同时,常用的,
∣a+b∣(a+b)⋅(a+b)∣a∣2+2a⋅b+∣b∣2=λ=λ2=λ2
即,
∣a∣2+2a⋅b+∣b∣2=∣a+b∣2
a⋅b=21(∣a+b∣2−∣a∣2−∣b∣2)
总结一下,上面两个式子,
a⋅b=41(∣a+b∣2−∣a−b∣2)
a⋅b=21(∣a+b∣2−∣a∣2−∣b∣2)
再结合点乘的定义,
a⋅b=∣a∣⋅∣b∣⋅cosθ
cosθ=∣a∣⋅∣b∣a⋅b
就可以求出向量夹角。
特殊的,
θ=0(cosθ=1),a⋅b=∣a∣⋅∣b∣
θ=π(cosθ=−1),a⋅b=−∣a∣⋅∣b∣
θ=π/2(cosθ=0),a⋅b=0
a⋅a=∣a∣2,∣a∣=a⋅a
经典的套路是,见模长便平方。
其中,第三条即,垂直向量向量点积等于零。
根据 cos90∘=0,a⊥b⟺a⋅b=0。
∣a⋅b∣≤∣a∣⋅∣b∣
当且仅当两向量共线,取等。
据此,可以判断两向量共线:
两个非零向量 a 与 b 共线,等价于,有唯一实数 λ,使得 b=λa。
由数乘的定义知,对于非零向量 a,如果存在实数 λ,使得 b=λa,那么 a∥b。
数值上,有判别式 a=λb⟺∣a⋅b∣=∣a∣∣b∣。
对于任意平面向量 a,b 有:
4a⋅b=(a+b)2−(a−b)2
常见形式为:
PA⋅PB=∣PM∣2−41∣AB∣2
其中 M 为 AB 中点。
若基底 e1,e2 不共线,则对于平面内任一向量 a,存在唯一实数 x,y 使得 a=xe1+ye2。
形式化的,平面内的任一向量都可以唯一的表示为两个不共线向量的线性组合。
存在性的证明:感性理解(雾
唯一性的证明,反证:假设存在两组实数 ⟨x1,y1⟩、⟨x2,y2⟩,
a=x1e1+y1e2=x2e1+y2e2
e1(x1−x2)=e2(y2−y1)
因为 x1=x2,y1=y2,则 e1,e2 共线,与条件不符,因此存在唯一性。
考虑构造性的证明,
若,
a⋅e1=a1,a⋅e2=a2
⟨e1,e2⟩=θ
设,a=xe1+ye2,用 a1,a2,θ 表示 a。
考虑,
e1e2=cosθ
a⋅e1=x+ye1e2=a1
a⋅e2=y+xe1e2=a2
列出方程组,
{x+ycosθ=a1y+xcosθ=a2
解得,
⎩⎨⎧x=sin2θa1−a2cosθy=sin2θa2−a1cosθ
这个思想很重要,常用一个很奇怪的式子,去点乘两个不共线向量。
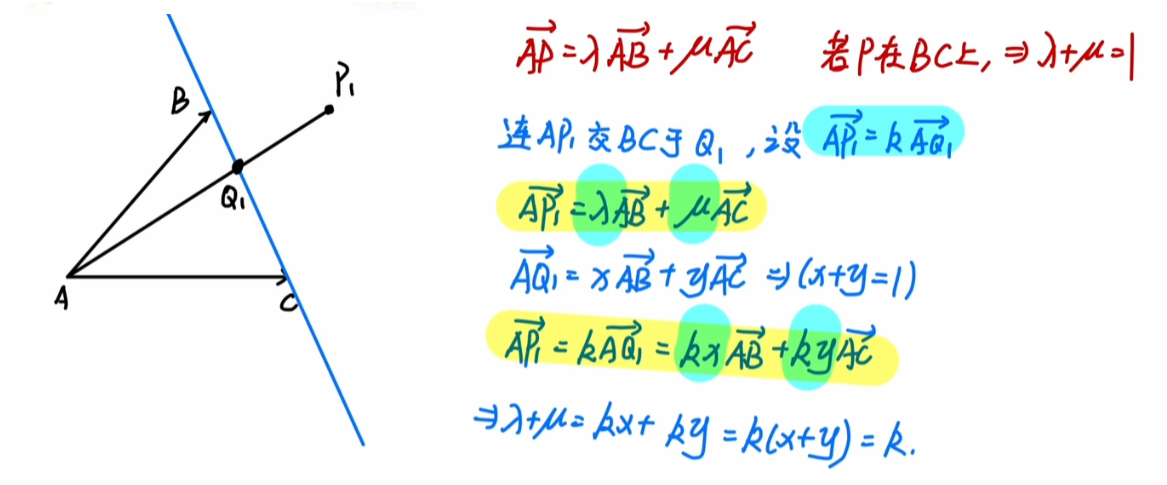
对于线段 AB 及一点 Q,若存在一点 O 满足,
OQ=λOA+(1−λ)OB
则 Q 在直线 AB 上,即 A,B,Q 三点共线。
证明如下:
AQOQ−OA=λAB=λ(OB−OA)
类似的,若 C 是线段 AB 中点,则对于任意一点 O,有,
OC=21OA+21OB
而坐标表示,(a,b) 与 (c,d) 平行,等价于 ad=bc。
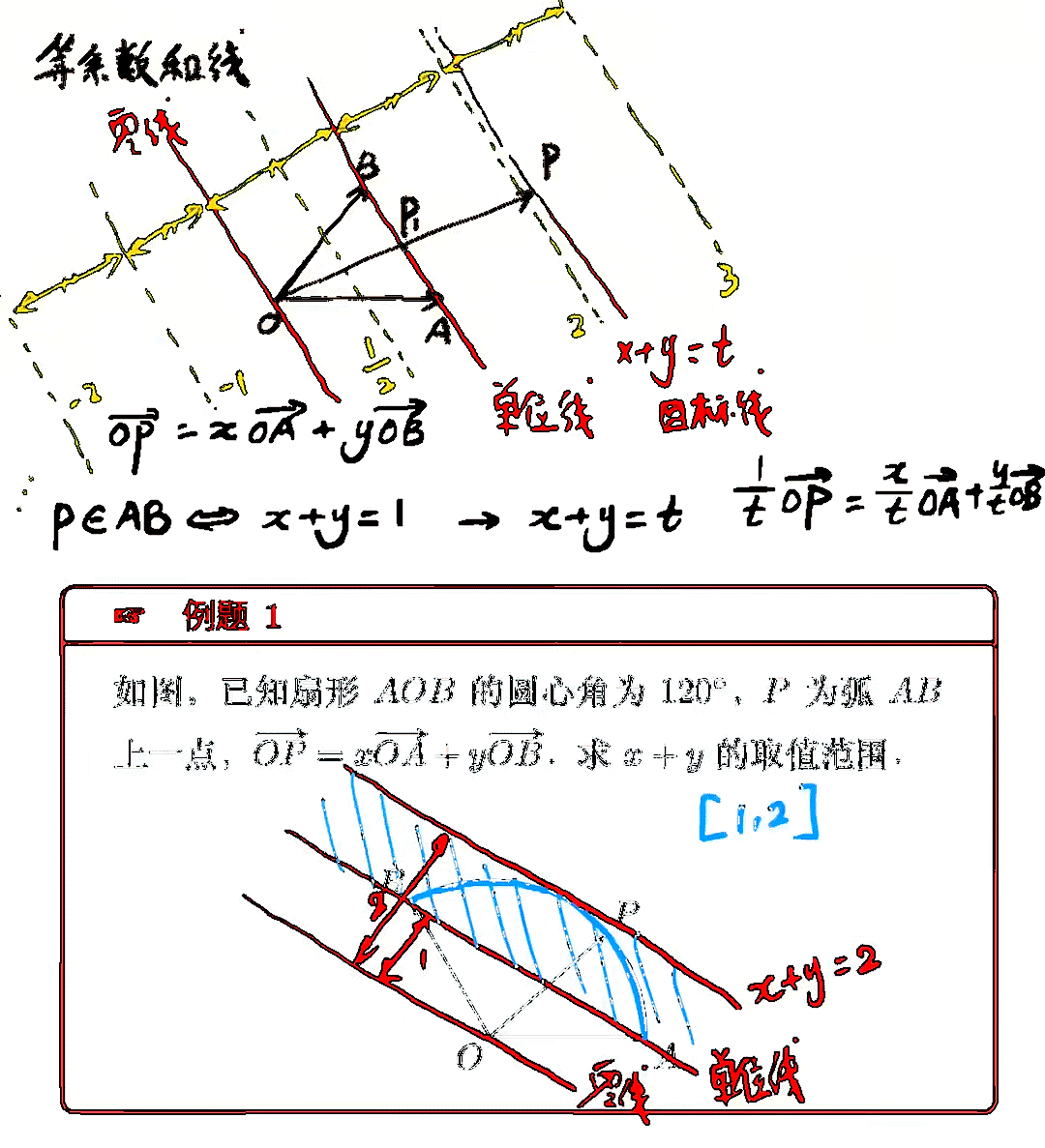
证明过程: