初高衔接

本章是一些初中不讲，但高中默认掌握的知识。

参考资料

• 乘法公式 - 维基百科
• 因式分解 - 维基百科

乘法公式

平方公式

在初中阶段，我们学过的 $3$ 个 平方公式：

1. 平方差公式

$$a^2-b^2=(a+b)(a-b)$$

2. 完全平方和公式

$$(a+b)^2=a^2+2ab+b^2$$

3. 完全平方差公式

$$(a-b)^2=a^2-2ab+b^2$$

立方公式

我们将 完全平方和公式 中的平方修改为 立方，得到：

1. 完全立方和公式

$$\begin{aligned} (a+b)^3 &= (a+b)(a+b)(a+b) \\ &= (a^2+2ab+b^2)(a+b) \\ &= a^3+2a^2b+ab^2+a^2b+2ab^2+b^3 \\ &= a^3+3a^2b+3ab^2+b^3 \end{aligned}$$

同理，将 完全平方差公式 中的平方修改为 立方，得到：

2. 完全立方差公式

$$\begin{aligned} (a-b)^3 &= (a-b)(a-b)(a-b) \\ &= (a^2-2ab+b^2)(a-b) \\ &= a^3-2a^2b+ab^2-a^2b+2ab^2-b^3 \\ &= a^3-3a^2b+3ab^2-b^3 \end{aligned}$$

将 完全立方和公式 移项，并提取公因式，得到：

3. 立方和公式

$$\begin{aligned} a^3+b^3 &= (a+b)^3-3a^2b-3ab^2 \\ &= (a+b)^3-3ab(a+b) \\ &= (a+b)((a+b)^2-3ab) \\ &= (a+b)(a^2-ab+b^2) \end{aligned}$$

同理，将 完全立方差公式 移项，并提取公因式，得到：

4. 立方差公式

$$\begin{aligned} a^3-b^3 &= (a-b)^3+3a^2b-3ab^2 \\ &= (a-b)^3+3ab(a-b) \\ &= (a-b)((a-b)^2+3ab) \\ &= (a-b)(a^2+ab+b^2) \end{aligned}$$

公式总结

这就是高中阶段常用的 $4$ 个 立方公式：

$$(a+b)^3=a^3+3a^2b+3ab^2+b^3$$ $$(a-b)^3=a^3-3a^2b+3ab^2-b^3$$ $$a^3+b^3=(a+b)(a^2-ab+b^2)$$ $$a^3-b^3=(a-b)(a^2+ab+b^2)$$

因式分解

因式分解是将一个多项式拆分为两个或多个因式相乘的过程。

公式法

将每一项凑成 乘法公式 的形式。

Example

Example 1

分解因式 $x^4-1$。

解得 $x^4-1=(x^2)^2-1^2=(x^2+1)(x^2-1)=(x^2+1)(x+1)(x-1)$。

Example 2

分解因式 $x^2+4y^2+4xy$。

解得 $x^2+4y^2+4xy=x^2+(2y)^2+2x(2y)=(x+2y)^2$。

十字相乘法

假设：

$$Ax^2+Bx+C=(ax+b)(cx+d)$$

展开：

$$Ax^2+Bx+C=(ax+b)(cx+d)=acx^2+(ad+bc)x+bd$$

将 $A$ 拆分为 $ac$，$C$ 拆分为 $bd$：

$$A=ac,C=bd$$

使其十字相乘后等于 $B$：

$$\begin{array}{c} a \\ b \end{array} \times \begin{array}{c} c \\ d \end{array}$$ $$B=ad+bc$$

Example

Example 1

分解因式 $x^2-x-6$。

$$\begin{array}{c} 1 \\ 1 \end{array} \times \begin{array}{c} 2 \\ -3 \end{array}$$

所以 $x^2-x-6=(x+2)(x-3)$。

Example 2

分解因式 $2x^2+9x-5$。

$$\begin{array}{c} 1 \\ 2 \end{array} \times \begin{array}{c} 5 \\ -1 \end{array}$$

所以 $2x^2+9x-5=(x+5)(2x-1)$。

Example 3

分解因式 $6x^2+7x-3$。

$$\begin{array}{c} 2 \\ 3 \end{array} \times \begin{array}{c} 3 \\ -1 \end{array}$$

所以 $6x^2+7x-3=(2x+3)(3x-1)$。

Example 4

分解因式 $x^2+(3-a)-3a$。

$$\begin{array}{c} 1 \\ 1 \end{array} \times \begin{array}{c} 3 \\ -a \end{array}$$

所以 $x^2+(3-a)-3a=(x+3)(x-a)$。

Example 5

分解因式 $x^2-2y^2+xy+x+5y-2$。

$$\begin{array}{c} 1 \\ 1 \end{array} \times \begin{array}{c} 2y-1 \\ 2-y \end{array}$$

所以 $x^2-2y^2+xy+x+5y-2=(x+2y-1)(x+2-y)$。

长除法

在解高次多项式方程时，如果已经找到一个根，就可以用 因式定理 把多项式拆成更简单的形式。

这样能一步步降低次数，方便继续求解：

1. 先找到多项式 $f(x)=0$ 的一个根 $a$。（尝试代入一些数，看结果是不是 $0$）
2. 根据因式定理，如果 $f(a)=0$，那么 $(x-a)$ 就是 $f(x)$ 的一个因式。
3. 用 长除法 把 $f(x)$ 除以 $(x-a)$，得到一个新的多项式 $g(x)$。
4. 除了 $x=a$ 以外，$f(x)=0$ 的其他解，正好都是 $g(x)=0$ 的解。
5. 因为 $g(x)$ 的次数比 $f(x)$ 低，继续求根会更简单。

Example

Example 1

分解因式 $x^3+2x^2-4x+1$。

注意到 $x=1$ 是方程的一个根：

$$\frac{x^3+2x^2-4x+1}{x-1}=x^2+3x-1$$

所以 $x^3+2x^2-4x+1=(x-1)(x^2+3x-1)$。

Example 2

分解因式 $x^3+x^2-3x-2$。

注意到 $x=-2$ 是方程的一个根：

$$\frac{x^3+x^2-3x-2}{x+2}=x^2-x-1$$

所以 $x^3+x^2-3x-2=(x+2)(x^2-x-1)$。

二重根式

利用 乘法公式 和 因式分解 的等式变形方法，可以化简二重根式（嵌套根式）。

引入

在解数学题时，有时会遇到一些二重根式的结果。

例如，在一个 $15\degree$ 的直角三角形中，两条直角边 $AB$ 和 $AC$ 分别为 $2+\sqrt 3$ 和 $1$。

现在要计算斜边 $BC$ 的长度。根据勾股定理：

$$BC=\sqrt{AB^2+AC^2}=\sqrt{(2+\sqrt 3)^2+1^2}=\sqrt{8+4\sqrt 3}$$

但这并不是最简答案，还可以进一步化简。

定义

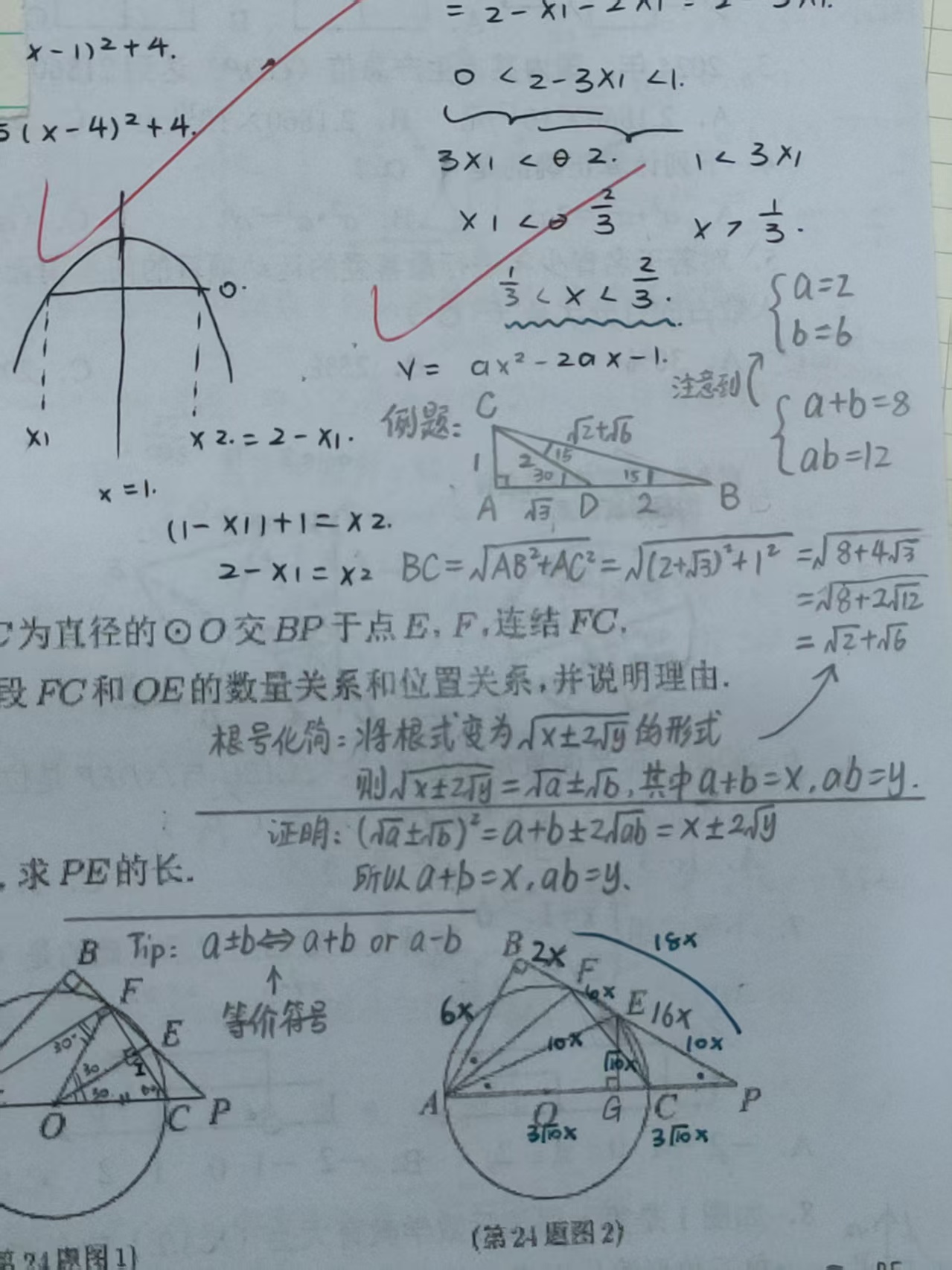
一般的二重根式的形式如下：

$$\sqrt{a\pm\sqrt b}$$

推导

我们设最终结果为 $\sqrt x+\sqrt y$：

$$\sqrt{8+4\sqrt{3}}=\sqrt{x}+\sqrt{y}$$

则有：

$$8+4\sqrt{3}=(\sqrt{x}+\sqrt{y})^2=x+y+2\sqrt{xy}$$

我们可以令：

$$x+y=8$$ $$2\sqrt{xy}=4\sqrt{3}$$

注意到一组正整数解：

$$x=2,y=6$$

所以化简结果为：

$$\sqrt{8+4\sqrt{3}}=\sqrt{2}+\sqrt{6}$$

总结

对于一般的二重根式：

$$\sqrt{a\pm\sqrt{b}}$$

找到一组正整数 $x$ 和 $y$，使得：

$$x+y=a,xy=\frac{b}{4}$$

这样就可以化简为：

$$\sqrt{a\pm\sqrt{b}}=\sqrt{x}\pm\sqrt{y}$$

tip

1. 并非所有的二重根式都能化简。
2. 能化简的结果也可能不止一个。

Example

Example 1

化简 $\sqrt{5-2\sqrt{6}}$。

$$\sqrt{5-2\sqrt{6}}=\left|\sqrt{2}-\sqrt{3}\right|=\sqrt{3}-\sqrt{2}$$

Example 2

化简 $\sqrt{4-\sqrt{15}}$。

$$\begin{aligned} \sqrt{4-\sqrt{15}} &= \frac{\sqrt{8-2\sqrt{15}}}{\sqrt{2}} \\ &= \left(\sqrt{5}-\sqrt{3}\right)\cdot\frac{\sqrt{2}}{2} \\ &= \frac{\sqrt{10}-\sqrt 6}{2} \end{aligned}$$

不等式

有些课程和教辅中会讲解不等式，但高中阶段也会学习相关内容，所以我将它们放在一起了。

详见 不等式