构造
参考资料
例题
洛谷 CF743C Vladik and fractions
构造一组 ,使得对于给定的 ,满足:
Code (1)
#include <bits/stdc++.h>
using namespace std;
using ll=long long;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin>>n;
if(n==1){cout<<-1<<'\n';return 0;}
cout<<n<<' '<<n+1<<' '<<n*(n+1)<<'\n';
return 0;
}
洛谷 CF1899F Alex's whims
树中两个顶点 和 之间的距离是指顶点 到顶点 必须经过的最小边数。
亚历克斯的生日快到了,蒂莫菲想送他一棵有 个顶点的树。然而,亚历克斯是个喜怒无常的孩子。在 天里,他每天都会选择一个整数,第 天选择的整数用 表示。如果在第 天,树上没有两片距离正好为 的叶子节点,亚历克斯就会很失望。
蒂莫菲决定送给亚历克斯一个设计器,这样他就可以随心所欲地改变他的树了。蒂莫菲知道亚历克斯也很懒惰,所以每天一开始,他可以进行仅仅一次以下类型的操作:
- 选择顶点 、 和 ,需要满足 和 之间有一条边, 和 之间没有边。然后删除 和 之间的边,并在 和 之间添加一条边。如果操作后图形不再是树,则不能执行此操作。
不知怎的,蒂莫菲设法找出了所有的 。之后,他又想出了一个绝妙的主意——以防万一,为这组集合 制作一本说明书,这样亚历克斯就不会失望了。
Solution



解题思路
如图,用 个节点构造一条链,根节点为 ,叶节点为 。(图中 )
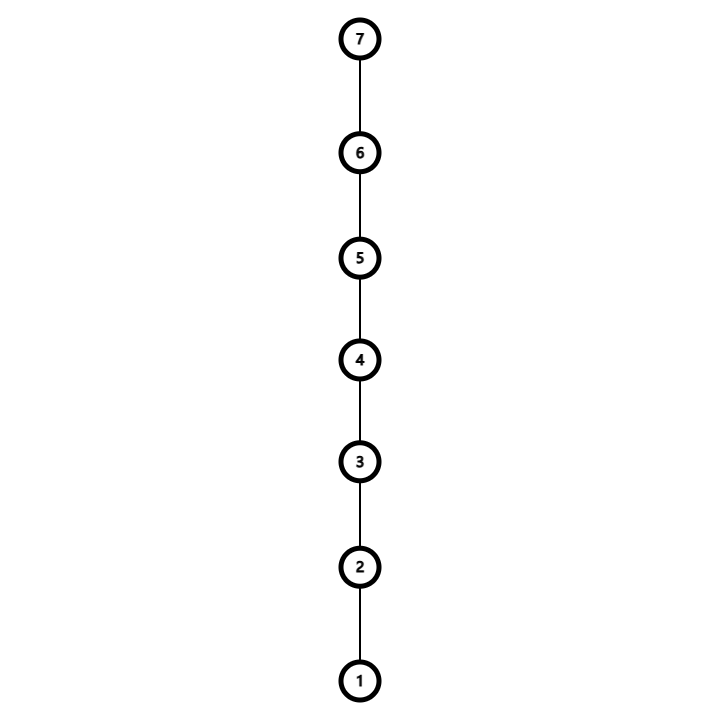
让动点 与节点 相连。显然,节点 也是叶节点。
节点 到节点 的距离为 ,节点 到节点 的距离为 ,所以节点 到节点 的距离刚好为 。
通过调整节点 的编号,即可得到距离为 的两个叶节点。
参考代码
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin>>T;
while(T--)
{
int n,q;
cin>>n>>q;
for(int i=1;i<n-1;i++)cout<<i<<' '<<i+1<<'\n';
cout<<n<<' '<<2<<'\n';
int now=2;
while(q--)
{
int d;
cin>>d;
if(d==now)cout<<-1<<' '<<-1<<' '<<-1<<'\n';
else cout<<n<<' '<<now<<' '<<d<<'\n';
now=d;
}
}
return 0;
}