数学：微积分

参考资料

• 积分 - 维基百科

约定

1. 为便于理解，本文中的所有函数均为常见的初等函数。
2. 数列的下标从 $1$ 开始。

引入

有一个 固定 的数列 $\set{A_1,A_2,\dots,A_n}$，需要 频繁 计算某个区间 $[a,b]$ 上的总和 $T$。

$$T=\sum_{i=a}^b A_i=A_a+A_{a+1}+\dots+A_b$$

如果每次都从 $A_a$ 累加到 $A_b$，运算总次数会很多，效率较低。如何更高效地计算呢？

前缀和

前缀和对于接触过算法竞赛（OI 或 ICPC）的读者应该并不陌生。

定义

由于数列是固定的，我们可以考虑 预处理。

预处理是指在正式计算之前，提前把一些可能 重复 用到的计算结果算好、存好。

这样之后计算就能更高效，不必重复做相同的事。

前缀和 就是一种常见的预处理技巧，提前计算出 前缀和数列 $S_n$：

$$S_k=\sum_{i=1}^k A_i=A_1+A_2+\dots+A_k$$

这样，前缀和数列 $S_k$ 就表示数列 $\set{A_n}$ 的前 $k$ 项和。

思想

利用前缀和，就可以高效计算任意区间 $[a,b]$ 的和：

$$\begin{aligned} T &= \sum_{i=a}^b A_i=A_a+A_{a+1}+\dots+A_b \\ &= (\sout{A_1+A_2+\dots+A_{a-1}}+A_a+A_{a+1}+\dots+A_b)-(\sout{A_1+A_2+\dots+A_{a-1}}) \\ &= \sum_{i=1}^b A_i-\sum_{i=1}^{a-1} A_i=S_b-S_{a-1} \end{aligned}$$

因此，通过预处理数列 $\set{A_n}$ 得到前缀和数列 $\set{S_n}$，可以高效区间求和：

$$T=\sum_{i=a}^b A_i=S_b-S_{a-1}$$

定积分

作用

对于简单图形，例如 长方形，当我们已知长宽为 $a$ 和 $b$ 时，可以使用 乘法 这个工具来计算其面积：

$$S=a\times b$$

对于更复杂的图形，例如边界是 曲线 的图形，就需要更高级的面积计算工具——定积分：

$$S=\int_a^b f(x)\mathrm{d}x$$

其中 $\displaystyle\int$ 称为 积分号，$a$ 称为 积分下界，$b$ 称为 积分上界，$f(x)$ 称为 被积函数，$\mathrm{d}x$ 称为 微分元。

定积分 $\displaystyle\int_a^b f(x)\mathrm{d}x$ 表示函数 $f(x)$ 图像在区间 $[a,b]$ 上与 $x$ 轴所围成图形的 有向面积：

$$S=\int_a^b f(x)\mathrm{d}x=|S_\text{蓝色}|-|S_\text{黄色}|$$

有向面积

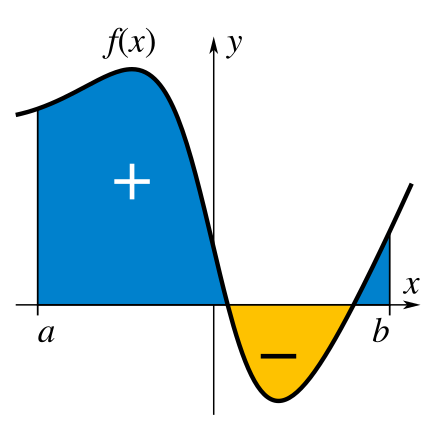
我们日常理解的“面积”都是正数，但在数学中引入了 有向面积 的概念，它可以为负。

在计算定积分时，我们约定：图像在 $x$ 轴 上方 的区域（蓝色）面积为 正，下方 的区域（黄色）面积为 负，这种带符号的面积叫作 有向面积。

这种表示方式在数学、科学，甚至生活中都很常见。

很多看似“只有大小”的量，其实也可以有正负之分，用来表示方向或性质。

例如角度、面积、长度、位移、海拔、温度、记账等。

tip

带符号有一个明显的优势：可以直接代入公式，自动处理方向，简化计算与判断。

海拔

一个人从海拔 $0$ 米出发，连续经过以下高度变化：

上升 $300$ 米；下降 $120$ 米；上升 $50$ 米；下降 $80$ 米；下降 $100$ 米；上升 $60$ 米。

如果不用正负号，每一步都要先判断方向，再决定加减，过程繁琐。

但如果用正负数来表示（上升为正，下降为负），变成：

$$(+300)+(-120)+(+50)+(-80)+(-100)+(+60)=110$$

这样，只需把这些数值直接相加，就能快速算出最终高度。

记账

一个人从余额 $0$ 元开始，连续经过以下收支变化：

收入 $300$ 元；支出 $120$ 元；收入 $50$ 元；支出 $80$ 元；支出 $100$ 元；收入 $60$ 元。

如果不用正负号，每一步都要先判断性质，再决定加减，过程繁琐。

但如果用正负数来表示（收入为正，支出为负），变成：

$$(+300)+(-120)+(+50)+(-80)+(-100)+(+60)=110$$

这样，只需把这些数值直接相加，就能快速算出最终余额。

角度

一个机器人从正前方（$0^\circ$）开始，连续经过以下旋转变化：

左转 $300^\circ$；右转 $120^\circ$；左转 $50^\circ$；右转 $80^\circ$；右转 $100^\circ$；左转 $60^\circ$。

如果不用正负号，每一步都要先判断方向，再决定加减，过程繁琐。

但如果用正负角度表示（左转为正，右转为负），变成：

$$(+300)+(-120)+(+50)+(-80)+(-100)+(+60)=110$$

这样，只需把这些角度直接相加，就能快速算出最终方向。

原理

这个符号可以理解为：从 $a$ 到 $b$ 将 无穷多个（$n\to\infty$）宽度为 $\mathrm{d}x$、长度为 $f(x)$ 的细长方形面积累加起来。

$$S=\int_a^b f(x)\mathrm{d}x$$

随着细长方形的数量增加，其总面积会越来越接近实际面积。

简单积分

对于一些简单图形的定积分，我们可以用公式直接计算。

Example

Example 1

计算 $\displaystyle\int_1^3 \frac{x}{2}\mathrm{d}x$。

这个积分表达式表示图中 直角梯形 的有向面积。

所以 $\displaystyle\int_1^3 \frac{x}{2}\mathrm{d}x=\frac{h(a+b)}{2}=\frac{2\cdot(0.5+1.5)}{2}=2$。

Example 2

计算 $\displaystyle\int_{-2}^3 2x\mathrm{d}x$。

这个积分表达式表示图中两个 三角形 的有向面积。

所以 $\displaystyle\int_{-2}^3 2x\mathrm{d}x=\frac{ah}{2}-\frac{bh}{2}=\frac{3\cdot 6}{2}-\frac{2\cdot 4}{2}=5$。

Example 3

计算 $\displaystyle\int_{-2}^2 \sqrt{4-x^2}\mathrm{d}x$。

这个积分表达式表示图中 半圆形 的有向面积。

所以 $\displaystyle\int_{-2}^2 \sqrt{4-x^2}\mathrm{d}x=\frac{1}{2}\pi r^2=\frac{1}{2}\pi\cdot 2^2=2\pi$。

不定积分

但对于更一般的定积分，无法直接求解。

定积分的定义并不复杂，就是函数 $f(x)$ 在区间 $[a,b]$ 的面积，但我们更关心的是如何计算它。

$$\int_a^b f(x)\mathrm{d}x$$

作用

前面我们已经通过对 数列 $\set{A_n}$ 做 前缀和，得到了 前缀和数列 $\set{S_n}$，从而高效区间求和：

$$S_n=\sum_{i=1}^n A_i$$ $$\underbrace{\set{A_n}}_{\text{数列}} \xrightarrow{\text{前缀和}} \underbrace{\set{S_n}}_{\text{前缀和数列}}$$

类似地，对于 函数 $f(x)$，我们也可以求“前缀和”，从某个 固定点 $c$ 开始，计算函数 $f(x)$ 在区间 $[c,x]$ 的面积，称为 原函数 $F(x)$：

$$F(x)=\int_c^x f(t)\mathrm{d}t$$ $$\underbrace{f(x)}_{\text{函数}} \xrightarrow{\text{积分}} \underbrace{F(x)}_{\text{原函数}}$$

这个类似“前缀和”过程叫做 积分，由于 $c$ 可以是任意常数，所以原函数有 无穷多个。

不定积分 $\displaystyle\int f(x)dx$ 表示所有可能的原函数，它们之间相差一个常数 $C$，称为 积分常数：

$$\int f(x)\mathrm{d}x=F(x)+C$$

tip

这里体现了有向面积的优势：无论 $x$ 与 $c$ 的大小关系如何，公式都能直接适用。

$$F(x)=\int_c^x f(t)\mathrm{d}t=-\int_x^c f(t)\mathrm{d}t$$

对比总结

数列可以看作定义域为正整数的特殊函数。

数列是离散的，函数是连续的。

对比	数列（离散）	函数（连续）
对象	$A_n$	$f(x)$
$[a,b]$ 区间“和”	$T=\displaystyle\sum_{i=a}^b A_i$ 求和	$S=\displaystyle\int_a^b f(x)\mathrm{d}x$ 定积分
方法	$S_n=\displaystyle\sum_{i=1}^n A_i$ 前缀和	$F(x)=\displaystyle\int_c^x f(t)\mathrm{d}t$ 积分
结果	$S_n$ 前缀和数列	$F(x)$ 原函数
计算	$T=S_b-S_{a-1}$	$S=F(b)-F(a)$

牛顿-莱布尼茨公式

现在，利用原函数，就可以计算 $f(x)$ 在区间 $[a,b]$ 的面积 $S$：

$$\begin{aligned} S &= \int_a^b f(x)\mathrm{d}x \\ &= \int_c^b f(x)\mathrm{d}x-\int_c^a f(x)\mathrm{d}x \\ &= F(b)-F(a)=\left.F(x)\right|_a^b \end{aligned}$$

其中 $F(b)-F(a)$ 也可以用 竖线求值符号 $\left.F(x)\right|_a^b$ 表示。

至此，我们得到了微积分学中最重要的公式——牛顿-莱布尼茨公式。

$$\int_a^b f(x)\mathrm{d}x=F(b)-F(a)=\left.F(x)\right|_a^b$$

微积分基本定理

微积分基本定理 是微积分学中的一条重要定理，由 艾萨克·牛顿 和 戈特弗里德·莱布尼茨 在十七世纪分别独立发现，描述了微积分的两个主要运算——微分 和 积分 之间的关系。

$$\text{微积分}=\text{微分}+\text{积分}$$

该定理分为两个部分，分别为 微积分第一基本定理 和 微积分第二基本定理，后者也被称为 牛顿-莱布尼茨公式。

刚才我们通过模仿数列前缀和的思路，找到了计算定积分的方法：先求出原函数，再计算两点的差值。

$$F(x)=\displaystyle\int_c^x f(t)\mathrm{d}t$$

要计算原函数 $F(x)$，首先需要了解 $f(x)$ 与 $F(x)$ 之间的关系。

差分

我们不妨先回到数列，考虑 $A_n$ 和 $S_n$ 之间的关系。

$$S_k=\sum_{i=1}^k A_i=A_1+A_2+\dots+A_k$$

如果已知 $S_n$，则有：

$$A_k=S_k-S_{k-1}$$

这个运算过程称为 差分。

而 前缀和 和 差分 互为逆运算：

$$\underbrace{\set{A_n}}_{\text{数列}} \xrightleftharpoons[\text{差分}]{\text{前缀和}} \underbrace{\set{S_n}}_{\text{前缀和数列}}$$

如果 $S_n$ 是 $A_n$ 的 前缀和数列，$A_n$ 就是 $S_n$ 的 差分数列。

前缀和表示数列前 $n$ 项的和，而差分表示数列每两项的差，也可以看作数列的 变化速度（变化率）。

微分

考虑什么东西能反映 函数 的变化速度（变化率）呢？

这就是高中阶段学过的 导数：

$$f(x)=\lim_{\Delta x\to 0}\frac{F(x+\Delta x)-F(x)}{\Delta x}$$

而 导数 就是微积分中的 微分。

tip

严格来说，导数 和 微分 是两个不同的概念，但它们的结果 完全相同。

• 导数：函数在某一点的瞬时变化率。
• 微分：当自变量发生微小变化时，因变量的近似变化量。

而 不定积分 和 微分 互为逆运算：

$$\underbrace{f(x)}_{\text{函数}} \xrightleftharpoons[\text{微分}]{\text{不定积分}} \underbrace{F(x)}_{\text{原函数}}$$

原函数的计算

回到最初的问题，如何计算原函数呢？

不幸的是，导数可以通过通用公式推导，但不定积分没有这样的通用公式，我们只能通过“凑”来求解。

许多现有的积分公式也是通过“凑”总结出来的。

如果已知函数 $F(x)$ 的导数是 $f(x)$，那么 $F(x)$ 就是不定积分 $f(x)$ 的一个原函数。

例题

Example

Example 1

计算 $\displaystyle\int_1^3 \frac{x}{2}\mathrm{d}x$。

$$\int_1^3\frac{x}{2}\mathrm{d}x=\left.\frac{x^2}{4}\right|_{1}^{3}=\frac{3^2}{4}-\frac{1^2}{4}=2$$

Example 2

计算 $\displaystyle\int_{-2}^3 2x\mathrm{d}x$。

$$\int_{-2}^3 2x\mathrm{d}x=\left.x^2\right|_{-2}^{3}=3^2-(-2)^2=5$$

Example 3

计算 $\displaystyle\int_{-2}^2 \sqrt{4-x^2}\mathrm{d}x$。

$$\int_{-2}^2\sqrt{4-x^2}\mathrm{d}x =\left.\left(2\arcsin\frac{x}{2}+\frac{x}{2}\sqrt{4-x^2}\right)\right|_{-2}^{2}=\pi-(-\pi)=2\pi$$