数学：微积分（咕）

定积分

有向面积

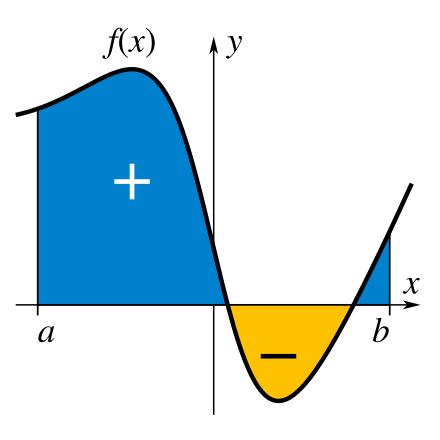
以前我们熟悉的“面积”通常都是正数，但数学中面积也可以是负数。

我们约定：位于 $x$ 轴 上方 区域（蓝色）的面积记为 正，下方 区域（黄色）面积记为 负。

定义

一些简单的图形，比如 长方形，当我们已知边长为 $a$ 和 $b$ 时，可以使用 乘法 这个工具来计算其面积：

$$S=a\times b$$

对于更复杂的图形，比如边界是 曲线 的图形，就需要更高级的面积计算工具——定积分。

简单来说，定积分 $\displaystyle\int_a^b f(x)\mathrm{d}x$ 表示函数 $f(x)$ 在区间 $[a,b]$ 上与 $x$ 轴所围成的 有向面积。例如上图：

$$\int_a^b f(x)\mathrm{d}x=S_\text{蓝色}-S_\text{黄色}$$

定积分的定义其实并不复杂，但我们要知道如何计算。

前缀和

前缀和对于学过算法竞赛的同学应该能轻松理解。

引入

思考：已知一个数列 $A_n$，有多次询问，如何快速求出其在区间 $[l,r]$ 上的总和？

$$\sum_{i=l}^r A_i=A_l+A_{l+1}+\cdots+A_r$$

有一种方法，我们可以将数列 $A_n$ 前 $n$ 项求和，记为 $S_n$。

$$S_n=\sum_{i=1}^n A_i=A_1+A_2+\cdots+A_n$$

此时，$S_n$ 就是 $A_n$ 的前缀和数列。

定义

前缀和是指数列前 $n$ 项的和，是一种常见的预处理技巧。

应用

通过前缀和，可以快速计算任意区间 $[l,r]$ 的和。

$$\sum_{i=l}^r A_i=S_r-S_{l-1}$$

数列与函数

数列是离散的函数，函数的连续的数列。

数列看作以正整数为定义域的函数。

不定积分

刚才我们利用前缀和的思想，已经可以快速求出数列的区间和。

而定积分是要给函数求“区间和”。

同理，我们可以像数列一样给函数求“前缀和”，而这个过程就是不定积分。

而不定积分可以理解为「函数 $f(x)$ 在区间 $[0,x]$ 的定积分」，即函数 $f(x)$ 在区间 $[0,x]$ 的面积。

微积分基本定理

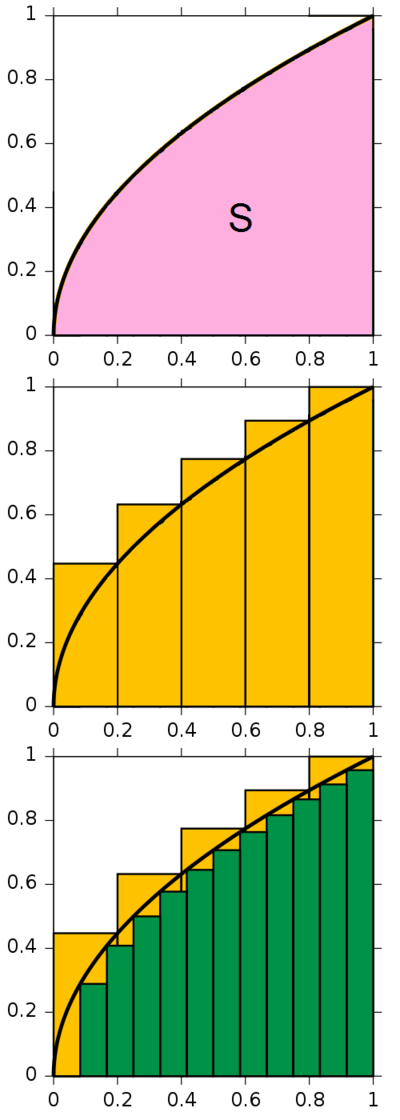
我们先不关心如何求不定积分。

假设我们已经知道 $F(x)$ 是 $f(x)$ 的不定积分。

仿照数列前缀和思想。

$\displaystyle\int_l^r f(x) \mathrm{d}x=F(r)-F(l)$

即 $[l,r] \text{ 的面积} = [0,r] \text{ 的面�积} -[0,l] \text{ 的面积}$。